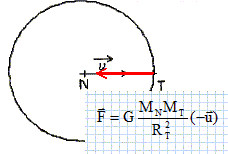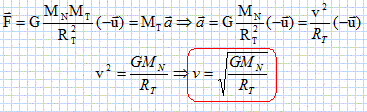Observation des satellites de Neptune par la sonde Voyager 2 ( bac S Afrique 2009)

Neptune est le dernier et le plus lointain des mondes géants que la sonde Voyager 2 nous fit découvrir. Cette planète porte le nom du dieu romain de la mer. Les photographies de la planète, par leur couleur bleue sombre, justifient pleinement cette association avec la mer. Voyager 2 survola Neptune et ses satellites les 24 et 25 août 1969 Neptune possède plusieurs satellites : Triton et Néréide figurent parmi les satellites les mieux connus. William Lassel a découvert Triton un mois après la découverte de la planète. C'est un satellite gros comme la lune ; il mesure environ 4200 km de diamètre. Il fait partie des plus gros satellites du système solaire après Ganymède, Titan et Callisto. L'orbite de Triton est circulaire autour du centre de Neptune. Découvert en 1949 Néréide est au contraire assez petit ( 320 km de diamètre) et a une orbite très elliptique, la plus allongée de tous les satellites. Néréide met 360 jours pour boucler son orbite. Voyager 2 a permis de localiser les six nouveaux satellites entre Neptune et Triton. D'après un article publié sur le site du Club Astro Antares. On donne : Neptune : masse : MN= 1,025 1026 kg ; Triton : masse : MT = 2,149 1022 kg ; rayon orbital : RT=3,547 105 km ; période de révolution Trév = 5,877 jours solaires. Période de rotation : Trot = 5,877 jourd solaires ; vitesse orbitale : v0 = 4 km/s. Néréide : demi-longueur du grand axe : a = 5513 103 km ; G = 6,67 10-11 m3 kg-1 s-2. 1 jour solaire = 86400 s. On considère que la planète Neptune et ses satellites sont des corps dont la répartition des masses est à symétrie sphérique. Les rayons ou les demi-grands axes des orbites sont supposés grands devant les dimensions de Neptune ou de ses satellites. Les mouvements des satellites. D'après le texte " Néréide est au contraire assez petit ( 320 km de diamètre) et a une orbite très elliptique". Choisir parmi les propositions suivantes le référentiel dans lequel est décrite cette orbite / héliocentrique ; néréidocentrique ; neptunocentrique ; géocentrique. Enoncer les première et deuxième lois de Kepler appliquées au cqs étudié ici. Première loi ou loi des orbites : dans le référentiel Neptuncentrique, l'orbite de chaque satellite est une ellipse dont l'un des foyers est le centre du soleil. Deuxième loi ou loi des aires : le mouvement de chaque satellite de Neptune est tel que le segment de droite reliant le centre de Neptune et le satellite balaie des aires égales pendant des durées égales. Placer sur la figure la demi-longueur du grand axe de Néréide. On considère les aires balayées par le segment reliant Neptune à Néréide pendant une même durée en différents points de l'orbite. 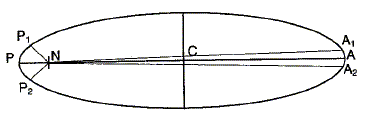Sur la figure ci-dessous, elles correspondent aux aires des surfaces formées par les points N, P1 et P2 autour du péricentre P d'une part et N, A1 et A2 autour de l'apocentre A d'autre part. 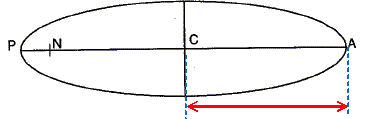Quelle relation relie ces aires ? D'après la seconde loi de Kepler, ces aires sont égales. Comparer alors les vitesses de Néréide aux points A et P. L'arc P1P P2 et l'arc A2A A1 sont parcourus pendant les mêmes durées. La longueur de l'arc P1P P2 et supérieure à la longueur de l'arc A2A A1 : la vitesse en P est donc supérieure à la vitesse en A. On souhaite déterminer la période de révolution Tner de Néréide. Enoncer la troisième loi de Kepler. Le carré de la période est proportionnel au cube du rayon de l'orbite. T2 / r3 = constante. Calculer la valeur de T2ner / R13 en s2 m-3. T2ner / R13 = T2T / RT 3 avec : RT=3,547 108 m ; TT = 5,877 jours solaires = 5,877*86400 =5,0777 105 s. T2T / RT 3 = (5,0777 105)2 / (3,547 108)3=5,77770 10-15 ~5,778 10-15 s2 m-3. En déduire la période de révolution de Néréide Tner et comparer a à la valeur donnée dans le texte. T2ner =5,77770 10-15 R13 avec R1 = a = 5,513 109 m. T2ner =5,77770 10-15 (5,513 109)3 =9,681 1014 ; Tner =3,111 107 s 3,111 107 / 86400 = 360,1 jours solaires, valeur en accord avec celle donnée dans le texte. Donner l'expression vectorielle de la force gravitationnelle exercée par Neptune sur Triton et calculer sa valeur. F = 6,67 10-11 * 1,025 1026 *2,149 1022 / (3,547 108)2 = 1,168 1021 ~1,17 1021 N. Le mouvement de Triton étant uniforme, en appliquant la seconde loi de Newton, établir l'expression littérale de sa vitesse v sur son orbite en fonction de MN, RT et G. Calculer cette vitesse et la comparer avec celle donnée dans l'énoncé. v = [6,67 10-11 * 1,025 1026 /3,547 108]½ = 4,39 103 m/s. En accord avec la valeur donnée dans l'énoncé (4 km/s, avec un seul chiffre significatif ). Montrer que la période de Triton Trév peut s'exprimer en fonction de MN, RT et G. La circonférence de rayon RT est parcourue à la vitesse v en une période Trév. 2 pi RT = v Trév Elever au carré : 4 pi2 RT2 = v2 T2rév Remplacer v2 par GMN/RT : 4 pi2 RT2 =GMN/RTT2rév T2rév = 4 pi2 RT3 /(GMN). Trév = 2 pi [RT3 /(GMN)]½. Calculer Trév et la comparer avec celle donnée dans l'énoncé. Trév = 2 *3,14 [(3,547 108)3 / (6,67 10-11 * 1,025 1026)]½ =5,08 106 s ou 5,08 106 / 86400 =5,87 jours solaires. En accord avec la valeur donnée 5,877 jours solaires.

retour -menu