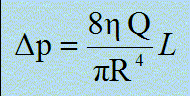Pertes de charges dans une seringue : Bernoulli, Poiseuille, Reynolds mécanique des fluides.

Soit une seringue horizontale de rayon intérieur R, de longueur L munie d'une aiguille de rayon intérieur r, de longueur l. Un piston coulisse sans frottement à l'intérieur de la seringue. Cette seringue est utilisée pour injecter un sérum de viscosité h dans les veines d'un patient. La pression dans la veine est pveine = 1,2 105 Pa. Comparer les pertes de charge dans l'aiguille DPA et dans la seringue DPS ? Calculer pour cela DPA/DPS en fonction de l, L, r et R. Dans l'hypothèse d'un écoulement laminaire la loi de Poisseuille s'écrit : DP : pertes de charge ( Pa) h : viscosité dynamique Pa s Q : débit molumique m3/s L : longueur (m) ; R rayon intérieur (m). Pertes de charge dans la seringue : DPS = 8h Q L / ( pR4) Il y a conservation du débit volumique Q. Pertes de charge dans l'aiguille : DPA = 8h Q l / ( pr4) DPA/DPS = lR4/ ( Lr4) = l/ L. (R/r) 4. Application numérique R= 10 mm ; r = 0,2 mm ; l= L/3 : DPA/DPS =  1/3 ( 10/0,2)4 =1/3*504 =1,67 105 ~ 1,7 105.  Les pertes de charge dans la seringue sont négligeables devant les pertes de charge dans l'aiguille. Il faut 10 s pour injecter 10 mL de sérum au patient. On donne la viscosité dynamique du sérum : h = 3 10-3 Pa s. Calculer les pertes de charges dans l'aiguille de longueur 2 cm. Le débit volumique d'écoulement du sérum est : Q = 10/10 = 1 mL s-1 = 10-6 m3 s-1. Appliquer la loi de Poisseuille pour le calcul des pertes de charges dans l'aiguille : DPA = 8h Q l / ( pr4) DPA =8*3 10-3 * 10-6 * 2 10-2 /[3,14*(2 10-4)4] =9,55 104 Pa~ 9,6 104 Pa. Quelle pression p doit exercer l'opérateur sur le piston pour injecter dans ces conditions le sérum ? Equation de Bernoulli avec perte de charge Dp : ½r(v22-v12) + r g(z2-z1) +p2-p1 = -Dp. z2-z1 = 0 seringue horizontale.  Le point (2) est situé à l'extrémité de l'aiguille au contact du sang de la veine. Le point (1) est situé sous le piston de la seringue. La section de la seringue étant 2500 fois supérieure à celle de l'aiguille, la vitesse v1 est négligeable devant v2. Par suite : ½r v22+ p2-p1 = -Dp. p1 = p2 +Dp+ ½r v22. Calcul de la vitesse v2 : v2 = Q/(pr2) =10-6 /(3,14*4 10-8) =7,96 ~ 8 m/s. En prenant r= 103 kg m-3, il vient : p1 = 1,2 105 + 9,6 104 +500*82 =2,48 105 ~ 2,5 105 Pa. p= p1-pression atmosphérique = 1,5 105 Pa. On considère une seringue de section S et de volume V rempli d'un liquide de masse volumique r. La seringue est munie d'une aiguille de section s et de longueur l. Le liquide est injecté dans une veine dans laquelle la pression dépasse de 15 mm de mercure la pression atmosphérique P0 = 105 Pa. V = 5 cm3 ; r = 103 kg m-3 ; S = 1 cm2 ; s= 0,2 mm2 ; l = 3 cm. L'infirmière doit exercée une force de 5 N sur le piston de la seringue. Calculer le travail fourni pour vider la seringue. La force étant constante et le déplacement ayant la même direction que la force, le travail est égal au produit de la force par le déplacement du piston de la seringue. déplacement = V/S = 5 /1 = 5 cm = 0,05 m. Travail = 5*0,05 = 0,25 J. On considère un écoulement laminaire dans l'aiguille. La vitesse moyenne d'éjection du liquide est v=0,5 m/s. Quel est le coeficient de viscosité du liquide. Pression exercée par l'infirmière : p = F/S = 5/ 10-4 = 5 104 Pa. Débit volumique : Q = v s = 0,5*2 10-7 = 10-7 m3 s-1. Surpression dans la veine : 15 mm Hg ; pveine = 15 10-3*13600*9,8 = 2 103 Pa En reprenant le résultat de l'exercice précédent : p1 = p2 +Dp+ ½r v22. Dp = p -pveine -½rv2 = 5 104 -2 103-500*0,52 =4,78 104 ~ 4,8 104 Pa. Appliquer la loi de Poisseuille pour le calcul des pertes de charges dans l'aiguille : DP = 8h Q l / ( pr4) h = DPpr4 / (8Q l ) avec r = (s/p)½ =(2 10-7 /3,14)½ =2,5 10-4 m. h =4,8 104 *3,14*(2,5 10-4)4 /(8*10-7 *3 10-2) =2,45 10-2 ~2,5 10-2 Pa s. Calculer le temps nécessaire pour vider la seringue. volume du liquide ( m3) / débit volumique ( m3 s-1) = 5 10-6 / 10-7 = 50 s.  Déterminer le nombre de Reynolds pour la seringue. Le nombre de Reynolds (sans unité) permet de déterminer si un écoulement est laminaire ou turbulent r : masse volumique du fluide (kgm-3) ; v : vitesse moyenne(ms-1), D : diamètre de la conduite (m) h = viscosité dynamique du fluide (Pa s) r = 103 kg m-3 ; h =2,5 10-2 Pa s ; D = 2(S/3,14)½ = 2(10-4/3,14)½ = 1,13 10-2 m La conservation du débit conduit à : vseringue = 0,5 *s /S = 0,5*0,2/100 = 10-3 m/s. Re = 103*10-3*1,13 10-2 / 2,5 10-2 =0,45.

retour -menu