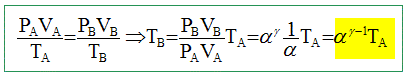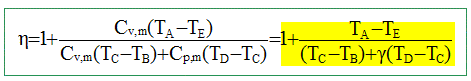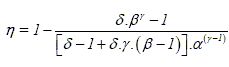Thermodynamique : moteur Diesel concours Mines 07

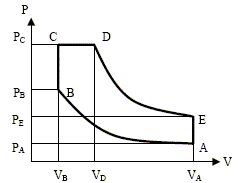
Les moteurs Diesel actuels fonctionnent suivant un cycle théorique modifié appelé cycle de Sabathé : la combustion s'effectue en deux étapes. Il est constitué des transformations suivantes : A-B : compression adiabatique réversible B-C : combustion isochore C-D : combustion isobare réversible D-E : détente adiabatique réversible E-A : détente isochore. On considère n moles de gaz supposé parfait décrivant le cycle et on pose : g= Cp,m /Cv,m avec Cp,m et Cv,m les capacités thermiques molaires à pression et volume constants a = VA /VB : rapport volumétrique de compression b = VD /VC : rapport volumétrique de combustion d = PC /PB : rapport de surpression de combustion Chaque état i sera caractérisé par Pi, Vi et Ti respectivement pression, volume et température.  Exprimer PB en fonction de PA, a et g. La transformation A--> B est adiabatique réversible. PAVAg=PBVBg. PB = PA[VA/VB]g ; PB =PAag. Exprimer TB en fonction de TA, a et g.   Déterminer les transferts thermiques échangés par n moles de gaz au cours de chaque transformation QAB , QBC , QCD , QDE , QEA en fonction des températures TA , TB , TC , TD , TE , des capacités thermiques molaires Cv,m , Cp,m et de n. A-B : compression adiabatique réversible donc QAB=0. B-C : combustion isochore : le travail échangé est nul ; la variation d'énergie interne du gaz est égal à QBC. L'énergie interne d'un gaz parfait ne dépend que de la température d'où QBC = nCv,m (TC-TB). C-D : combustion isobare réversible La variation d'enthalpie est égale à QCD. QCD = n Cp,m( TD-TC). D-E : détente adiabatique réversible donc QDE=0. E-A : détente isochore : le travail échangé est nul ; la variation d'énergie interne du gaz est égal à QEA. L'énergie interne d'un gaz parfait ne dépend que de la température d'où QEA = nCv,m (TA-TE). Après avoir défini le rendement thermodynamique (ou efficacité thermodynamique) pour un moteur que l’on notera h, l’exprimer en fonction des températures et de g. rendement = travail fourni / énergie prélevée à la source chaude. h = -W / (QBC + QCD). Travail fourni au cours du cycle : W énergie mise en jeu au cours du cycle : QBC + QCD + QEA. La variation d'énergie interne est nulle sur le cycle : W+QBC + QCD + QEA=0 -W = QBC + QCD + QEA h= [QBC + QCD + QEA] / [QBC + QCD] = 1+QEA / [QBC + QCD]   Montrer que h peut se mettre sous la forme : Il faut exprimer toutes les températures en fonction de TA afin de pouvoir simplifier numérateur et dénominateur par TA : TB= TA ag-1. La transformation BC est isochore d'où : PC/TC=PB/TB soit PC/PB=TC/TB = d. TC= dTB = dTA ag-1. La transformation CD est isobare d'où : VC/TC=VD/TD soit VD/VC=TD/TC = b. TD= bTC = bdTA ag-1. La transformation DE est adiabatique réversible : TE VEg-1 = TD VDg-1. La transformation EA est isochore : VE = VAsoit TE VAg-1 = TD VDg-1. TE = TD [VD /VA ]g-1. Or a = VA /VB ; b = VD /VC ; VB =VC d'où VD /VA = b / a. par suite : TE = TD [b / a ]g-1 = bgdTA. TA-TE = TA[ 1-bgd] TC-TB = dTA ag-1-TA ag-1 = TA[ d -1]ag-1. TD-TC = bdTA ag-1- dTA ag-1 =TA[ b -1]dag-1. g(TD-TC) =TA[ b -1]dgag-1.

retour -menu