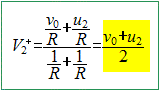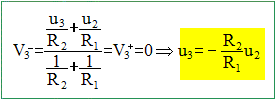chaîne électronique de mesure de température, sonde de platine concours Mines 07

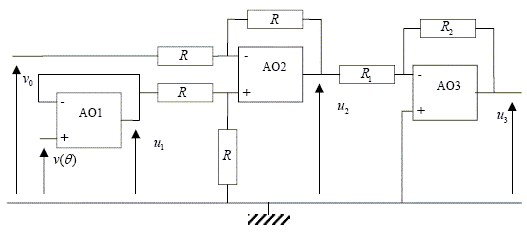
On construit une chaîne électronique avec trois amplificateurs opérationnels. La tension v(q) est fournie par un capteur de température qui ne peut délivrer de courant électrique. Cette tension est seulement fonction de la température q et elle est donnée avec précision par : v(q) = v0-aq. avec v0=0,7 V et a= 2mV °C-1, les résistances ont pour valeurs R1=2 kW et R2 = 1 kW. Les trois amplificateurs sont supposés parfaits et fonctionnent en régime linéaire : rappeler les caractéristiques de tels amplificateurs. Les tensions d'entrée V+ et V- sont égales ; les intensités des courants d'entrée sont nulles. Quelle relation y a-t-il entre u1 et v(q) ? Quel est le rôle de ce premier étage (AO1) ? Le premier étage est un montage suiveur : u1=v(q).  Le capteur de température ne peut pas fournir de courant : l'étage n°1 permet de garder la tension fournie par le capteur et délivre un courant à la sortie.  Exprimer u2 en fonction de v0 et u1 , puis en déduire u2 en fonction de la température q. Théorème de Millman : 2V2- = u1 ; V2- = V2+ d'où u1= v0+u2 ; u2 = u1- v0 : étage soustracteur Or u1=v(q) et v(q) = v0-aq d'où u2 = -aq. Exprimer u3 en fonction de u2. En déduire la relation entre u3 et la température q.   u3 = R2/R1 aq. Quel est l’intérêt d’utiliser un millivoltmètre pour mesurer la tension de sortie du montage. R2/R1 = 0,5 ; a = 2 mV °C-1 ; u3 = q. avec u3 en mV et q en °C. La lecture de la tension en mV donne la température en °C. Température et résistance de platine. 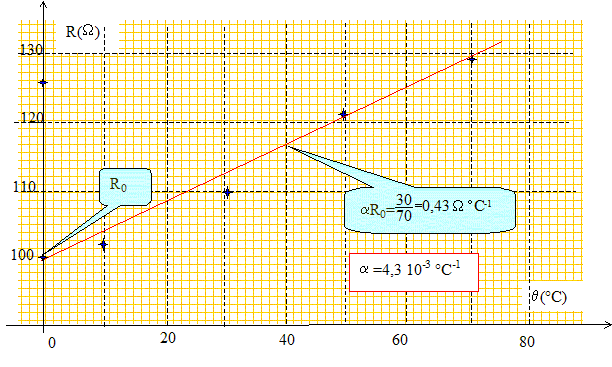Les capteurs « résistance de platine Pt100 » sont très utilisés pour mesurer les températures d’un milieu liquide. Le principe repose sur une relation quasi affine (dans un certain domaine de température) entre la résistance R et la température q. R(T) = R0(1+aq). Différentes mesures de R en fonction de T sont consignées dans le tableau suivant : R(W) 101 103 110 122 129 q(°C) 0 10 30 50 70 Justifier, par ses propriétés physicochimique, l'emploi du platine. Métal inaltérable présentant, de plus, une bonne résistance mécanique. Représenter la courbe R=f(q). En déduire R0 et a. Au moment de l’immersion de la résistance à la température T0 dans un liquide à la température Tl , l’équilibre thermodynamique n’est pas réalisé. On se propose d’étudier la variation de T en fonction du temps. En notant c la capacité thermique massique du platine, exprimer le transfert thermique reçu dQr par le platine pour une variation infinitésimale de la température dT. dQr= c dT. Les pertes thermiques du capteur, pendant une durée dt, sont caractérisées par un transfert thermique dQp= ß(T-Tl)dt. Etablir l’équation différentielle entre T et t, puis la résoudre. dQr + dQp= 0 ; c dT + ß(T-Tl)dt=0 c dT /dt + ßT = ßTl. (1) Solution générale de l'équation sans second membre : T= A exp(-b/c) Solution particulière de (1), régime permanent : T= Tl. Solution générale de (1) : T= A exp(-bt/c)+ Tl. à t=0, T=T0 d'où A = T0 -Tl. T= (T0 -T1)[1- exp(-bt/c)] +T1.   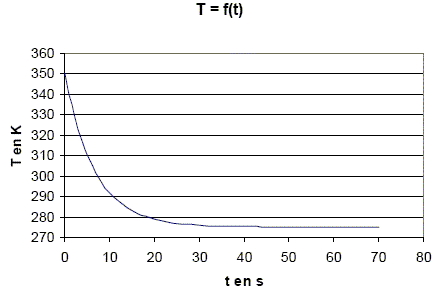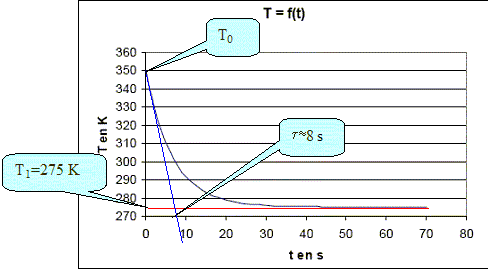On obtient la courbe suivante : En déduire les valeurs de T0, T1 et définir une constante de temps t, l’évaluer et en déduire la valeur de ß. t = c/b ; b =c/t avec c = 133 J K-1 kg-1. b = 133/8 = 17 J K-1 kg-1 s-1.

retour -menu