Aurélie 22/01/08
 

Mesure d'une focale : viseur, oeil normal, oeil myope concours Mines 07

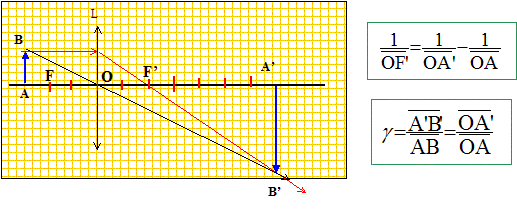
Les distances algébriques sont écrites en gras et en bleu. 

On considère une lentille mince de centre O dans l’approximation de Gauss.

Préciser la signification des deux termes en gras.

L'objet doit être de petites dimensions et placé au voisinage de l'axe optique principal du système optique.

On élimine ainsi les rayons lumineux trop inclinés sur l'axe optique.

Rappeler la formule de conjugaison de Descartes pour une lentille mince donnant la position de l’image OA' en fonction de celle de l’objet OA.

Etablir l’expression du grandissement en fonction de OA et OA'.

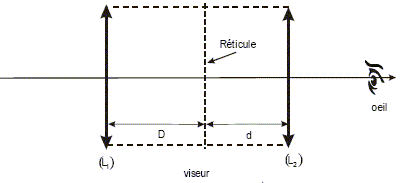
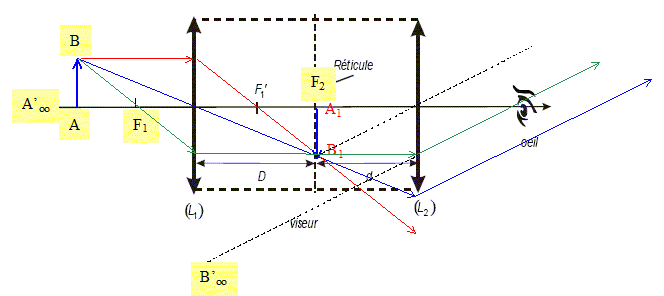
Dans les triangles semblables OAB et OA'B' : A'B' / AB = OA' / OA.

Un viseur à frontale fixe est constitué :

• d’un objectif, constitué d’une lentille mince L1 convergente de centre O1 et de distance focale image, f'1 = 7,0 cm,

• d’un réticule distant d’une distance D =14 cm de l’objectif,

• d’un oculaire constitué d’une lentille mince L2 convergente de centre O2 et de distance focale image f'2 = 3,0 cm,, située à la distance d du réticule.

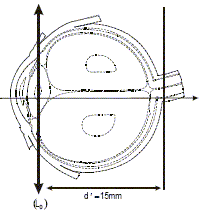
Un oeil « normal » voit sans accommodation à l’infini. En déduire la distance d pour que l’oeil puisse voir le réticule sans accommoder.

L'image intermédiaire A1B1 donnée par L1 de l'objet AB doit se trouver dans le plan focal objet de L2.

A1B1 sert d'objet pour L2 : A1B1 étant dans le plan focal objet de L2, l'image donnée par cette lentille, est à l'infini. Donc d = 3,0 cm.

Un oeil myope est modélisable par une lentille L0 ( convergente dont le centre optique O est placé à d'=15 mm de la rétine, modélisé par un écran. Sa faculté d’accommodation lui permet d’adapter sa focale : il obtient une image nette lorsque l’objet est situé à une distance comprise entre d1 = 12 cm (punctum proximum) et d2 = 1,2 m (punctum remotum) de L0.
 

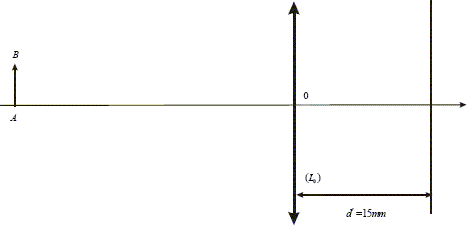
Quelle doit être la valeur de la focale image f'0 de L0 pour obtenir une image nette sur la rétine d’un objet situé à une distance d= 12 cm (punctum proximum) devant l’oeil ?

OA' = 15 mm = 0,015 m ; OA = -0,12 m

La relation de conjugaison des lentilles minces donne : 1/f'0 = 1/OA' -1/OA =1/0,015 + 1/0,12 = 75

f'0 = 1/75 = 0,0133 m = 1,33 cm.
Quelle doit être la valeur de la focale image f'0 de L0 pour obtenir une image nette sur la rétine d’un objet situé à une distance d= 1,2 m (punctum remotum) devant l’oeil ?  

OA' = 15 mm = 0,015 m ; OA = -1,2 m

La relation de conjugaison des lentilles minces donne : 1/f'0 = 1/OA' -1/OA =1/0,015 + 1/1,2 = 67,5

f'0 = 1/67,5 = 0,0148 m = 1,48 cm.

Déterminer graphiquement, dans le cadre de l'approximation de Gauss, les positions des foyers image, F' et objet de la lentille sur la figure ci-dessous :

On accole l’oeil myope à l’oculaire. On admettra que l’oeil accommode à son punctum remotum.

Où doit se trouver l’image définitive à la sortie du viseur ?

L'image du réticule, donnée par l'oculaire doit se trouver à d= 1,2 m devant l'oeil myope pour obtenir une image définitive nette sur la rétine.

En déduire la nouvelle distance d entre le réticule et l’oculaire.

  1/f'2 = 1/OA' -1/OA avec OA' = -1,2 m, f'2 = 0,03 m

1/OA = 1/OA' - 1/f'2 =-1/1,2 -1/0,03 = -34,167 ; OA = -1/34,167 = -0,0293 m = - 2,93 cm.

On cherche à voir simultanément l’objet visé et le réticule.

Où doit-on placer un objet pour pouvoir le voir à travers le viseur ?

Objet visé et réticule doivent être conjugués l'un de l'autre pour la lentille L1, l'objectif.

Ecrire la relation de conjugaison pour L1 avec OA' = D.

1/f'1 = 1/OA' -1/OA soit 1/OA = 1/D- 1/f'1 ; OA = f'1 D / (f'1-D).

OA = 7 *14/(7-14) = -14 cm.

L'objet est situé 14 cm à gauche de l'objectif.

Cette position dépend-elle de la nature de l’oeil (« normal » ou myope) ?

Non : l'image intermédiaire est située dans le plan du réticule ; le déplacement de l'oculaire permet de voir cette image nette, que l'oil soit normal ou myope.

 

Lorsque un oeil « normal » n’accommode pas, faire la construction de la position de l’objet.

L'image définitive est à l'infini ; l'image intermédiaire est au foyer objet de l'objectif.

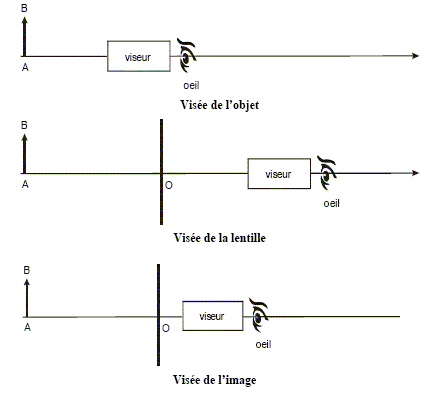
Justifier le nom de « viseur à frontale fixe».

Ce viseur donne une image nette d'un objet situé à 14+D=28 cm devant le réticule.

Le viseur est utilisé pour mesurer la distance focale d’une lentille L de focale f' inconnue.

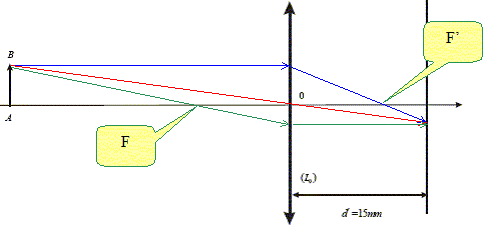
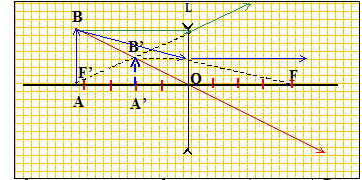
La 1ère étape est la visée de l’objet, AB. On place ensuite la lentille inconnue après l’objet et on vise le centre O de la lentille. Pour cela, nous devons reculer le viseur de x1 = 20 cm. Pour la visée de l’image A'B' à travers la lentille, nous avançons le viseur de x2 = 10 cm.

Préciser les valeurs algébriques OA et OA'.

Le point O est visé en reculant le viseur : OA = -0,20 m

La visée de l'image est obtenue en avançant le viseur : OA' = -0,10 m

En déduire la distance focale f' de la lentille.

Formule de conjugaison : 1/f' = 1/OA' -1/OA = 1/(-0,1) -1/(-0,2) = -10+5 = -5 ; f' = 1/(-5) = -0,2 m = -20 cm.

La distance focale image étant négative, la lentille est divergente.

Faire la construction de l’image à travers cette lentille inconnue L.

retour -menu