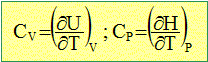Capacité thermique, entropie, cycle moteur. concours mines 06

sans calculatrice.

On définit une capacité calorifique à volume constant C_V, et une capacité calorifique à pression constante C_P.

Rappeler les définitions de C_V et C_P.

C_V : énergie nécessaire pour élever la température d'une mole de corps pur de 1 kelvin, à volume constant.

C_P : énergie nécessaire pour élever la température d'une mole de corps pur de 1 kelvin, à pression constante.

Proposer en quelques lignes une méthode simple pour mesurer C_P.

Mesurer, à pression constante, la différence de température consécutive à un échange thermique donné.

Pour un solide, ces deux capacités sont considérées comme identiques. Pour quelle raison ?

Peut-on identifier C_P et C_V pour un gaz ? Pourquoi ?

La dilatation des solides est faible.

Les gaz subissent de forte dilatation et dans ce cas C_P est différent de C_V.

Quelle relation relie C_P et C_V pour un gaz parfait ?

Pour n moles d'un un gaz parfait, C_P-C_V= nR.

Le baromètre, assimilé à un corps solide de capacité calorifique C=C_P=C_V, est initialement à une température T₁. On le plonge dans un lac dont la température T₀ est constante et on attend l’équilibre thermique. On définit la variable x par : x= T₁/T₀.

Exprimer la variation d’entropie du baromètre DSB en fonction de C et de x. dSB = d QB/T = CdT/T = C d(lnT) intégrer entre T1 et T0 : DSB = C ln(T0/T1) = -C ln x.

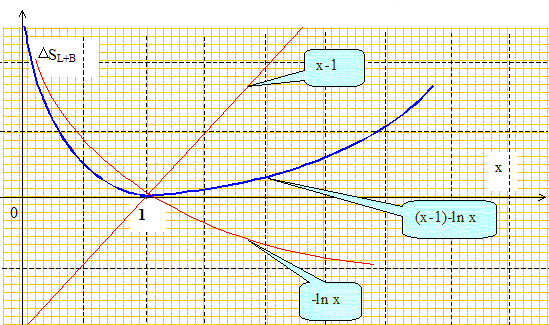
Exprimer la variation d’entropie du lac DS_L en fonction de C et de x.

dS_L = -d Q_B/T₀= -CdT/T₀ ; intégrer entre T₀ et T₁ :

DS_L = C(T₁-T₀) / T₀ = C(x-1).

La variation d’entropie de l’ensemble « baromètre + lac » est : DS_L+B =C [(x-1) - ln x] .

Montrer graphiquement que DS_L+B est toujours positive.

C est positif ; x= T₁/T₀. 

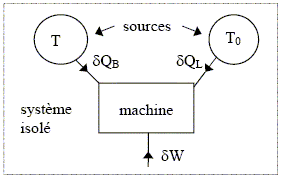
Le baromètre est initialement à une température T₁. On dispose d’un lac dont la température T₀ est constante, avec T₁ > T₀.

A l’aide de ces deux sources, on fabrique un moteur dont la machine effectue des cycles réversibles.

Le schéma classique de ce moteur figure ci-dessous.

Soient d Q_B et d Q_L les transferts thermiques échangés par la machine avec le baromètre et avec le lac, et d W le travail du moteur fourni au cours d’un cycle.

Au cours d’un cycle, la température du baromètre passe de la valeur T (comprise entre T₁ et T₀) à la température T + dT.

 Quelle relation a-t-on entre dW, d Q_B et d Q_L ?

La variation d'énergie interne est nulle sur le cycle. Le premier principe s'écrit :

d W + d Q_B+dQ_L=0. (1)

Quelle relation a-t-on entre d Q_B, d Q_L, T et T₀ ?

La variation d'entropieest nulle sur le cycle. Le second principe s'écrit, pour un système réversible :

d Q_B/T+dQ_L/T₀=0. (2)

Le moteur s’arrête de fonctionner lorsque la température du baromètre atteint la valeur T₀.

Exprimer alors les valeurs de Q_B, Q_L en fonction de T₁ et T₀.

d Q_B = -C dT ; intégrer entre T₁ et T₀ :

Q_B = -C(T₀ -T₁ ).

(2) donne : d Q_L = -d Q_BT₀ /T = C T₀dT /T = C T₀d ln T ; intégrer entre T₁ et T₀ :

Q_L = C T₀ ln (T₁/T₀).

Définir le rendement de ce moteur en fonction de W et Q_B, puis en fonction de C, T₁ et T₀.

 rendement : travail obtenu divisé par l'énergie reçue de la part de la source chaude.

h= -W/Q_B ;

(1) donne -W= Q_B+Q_L ; h= 1+Q_L / Q_B.

h= 1-T₀ ln (T₁/T₀) /(T₀ -T₁ ).