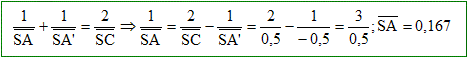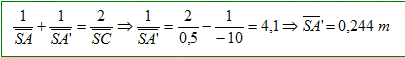Aurélie 11/12/07
 

optique : les rétroviseurs: miroir plan, miroir sphérique concours mines 06

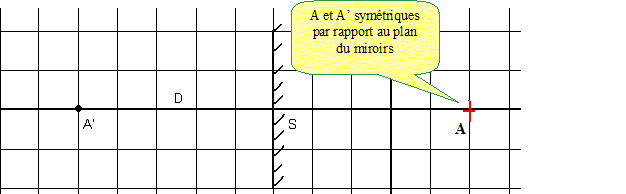
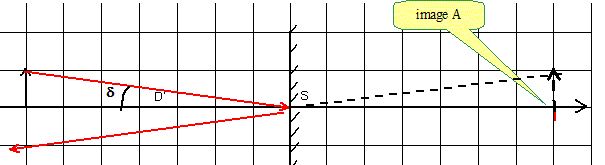
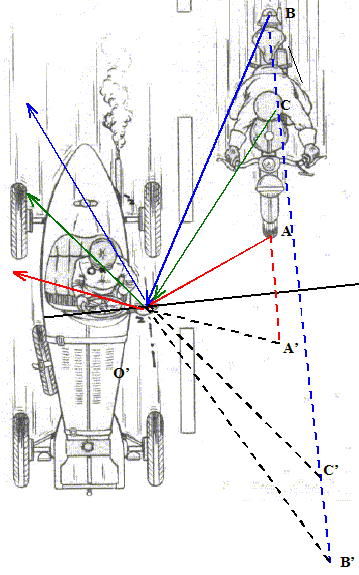
Le champ d’un miroir est la portion de l’espace qu’un observateur voit dans un miroir. Ainsi, un rétroviseur de voiture ne permet pas au conducteur de voir une autre voiture qui se situerait hors de cette portion ; c’est ce que l’on appelle l’angle mort.

Le rétroviseur est un miroir plan.

Le rétroviseur est un miroir plan de largeur L. L’observateur place son oeil, supposé ponctuel, en un point A’ de l’axe du miroir à une distance D de celui-ci.

Positionner le point A dont l’image est A’ par le miroir.

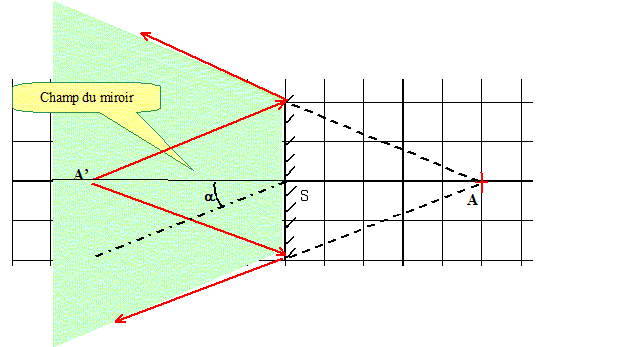
Où se situent les points que l’observateur peut espérer voir par réflexion dans le miroir ? Faire apparaître cette portion d’espace sur la construction.

Préciser la valeur de l'angle b qui caractérise la portion d'espace accessible à la vision ; c'est le champ du miroir.

b = 2 a et tan a = L/(2D)

Application numérique : calculer b, avec L = 20 cm , D = 50 cm.

tan a = L/(2D) =20/100 = 0,20 ; a =11,3 ; b = 22,6 °.

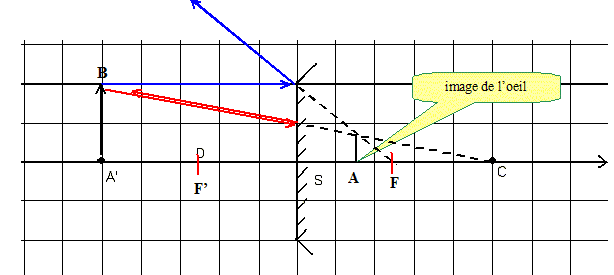
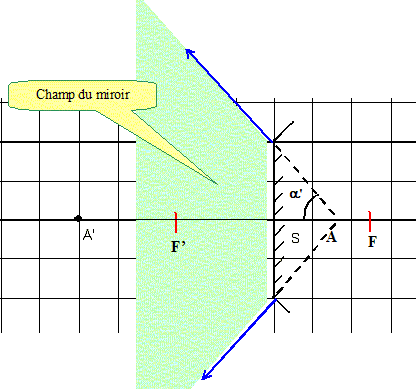
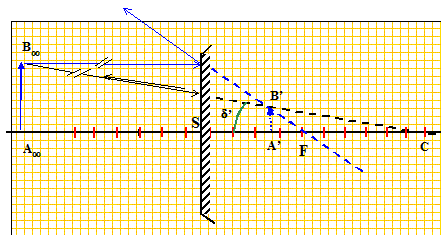
Le rétroviseur est un miroir sphérique convexe.

Le miroir plan est remplacé par un miroir sphérique convexe, de rayon de courbure R = 50 cm et de même largeur L. L’oeil de l’observateur est toujours placé en A’

 Effectuer la construction graphique du point A dont l’image est A’ par le miroir.

Faire apparaître le champ du miroir sur la construction.
 

Préciser la valeur de l'angle b' qui caractérise le champ de vision.

Application numérique : calculer b', avec L = 20 cm , D = 50 cm, R = 50cm.

b' = 2 a' et tan a' = L/(2SA)

L'objet, l'oeil est situé à SA'=-0,5 m ; SC=+0,5 m ;

tan a' = D/(2SA)= 0,2/0,333 =0,6

a' = 31° ; b' =62°.

 

Comparaison des deux dispositifs.

Comparer les champs angulaires des deux types de rétroviseur.

L'angle b' est presque trois fois plus grand que l'angle b.

Le champ angulaire est très important dans le cas du miroir sphérique ( par rapport au miroir plan).

Un objet, de taille 1m, est situé à une distance D’ = 10 m du rétroviseur.

Faire une construction graphique de l’image dans les deux cas.  

 

L'image et l'objet ont la même taille. ( symétrie par rapport au plan du miroir )

 

SA=-10 m ; SC=+0,5 m

Taille de l'image : SA'/SA = 0,244/10 = 0,024 m = 2,4 cm.

Déterminer puis calculer les angles apparents sous lesquels l’automobiliste voit l’objet avec les deux types de rétroviseur. Commenter.

miroir plan : tan d = 1/10 = 0,1 ; d = 0,1 rad.

miroir sphérique :

Dans le cas du miroir sphérique, l'objet peut être considéré comme étant à l'infini. L'image est alors au foyer F.

 d'=A'B' / FC = 0,024 / 0,25 = 0,096 rad.
Angle mort

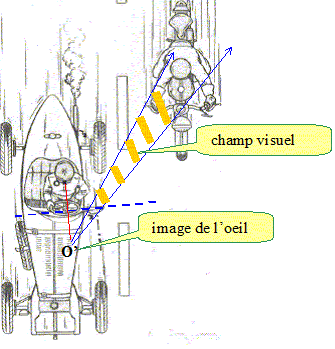
Le motard est-il vu dans le rétroviseur de l’automobiliste ?

Vous justifierez votre réponse à l’aide d’un tracé. Le rétroviseur est considéré comme un miroir plan, son axe étant symbolisé par NN’ sur la figure. Les yeux du conducteur sont représentés par le point O.

La partie avant de la moto ( de A à C) est invisible. De même que la partie arrière ( de C à B).

Par contre la tête du motard est visible : la lumière issue de C passe par l'oeil après réflexion sur le miroir.

retour -menu