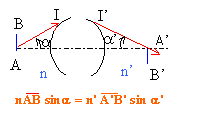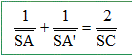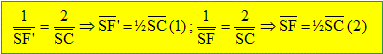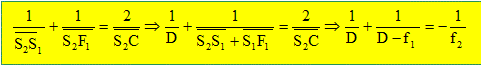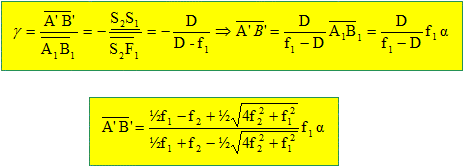|
Miroir sphérique, télescope de Cassegrain concours Mines 05 |
|||||||
|
|||||||
|
Stigmatisme rigoureux pour un couple de points A et A' conjugués : tous les rayons issus de A passent par A'. aplanétisme : condition d'Abbe le stigmatisme doit être rigoureux pour le couple A et A' et le couple B et B'; B et B' se trouvant dans un plan de front.
On considère un miroir sphérique concave de centre C et de sommet S. Un objet AB assimilable à un segment est placé perpendiculairement à l'axe optique, l'extrémité A étant située sur cet axe. Construire, dans le cadre de l'approximation de Gauss, l'image A'B' de AB.
Tout rayon incident : - passant par C se réfléchit sur lui même - passant par le sommet S donne un rayon réfléchi symétrique du rayon incident par rapport à l'axe optique CS. - parallèle à CS donne un rayon réfléchi passant par le foyer F'. Etablir à l’aide de
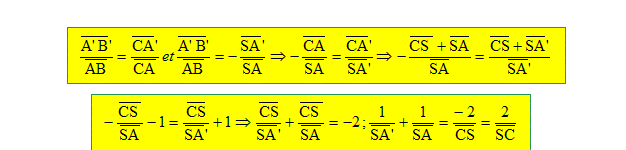
cette construction les formules suivantes de conjugaison
avec origine au sommet :
En déduire l'existence d'un foyer objet F et d'un foyer image F' et préciser leurs positions relatives par rapport ' S et C. L'image d'un objet situé à l'infini se trouve au foyer image F' (1) Un objet se trouvant au foyer objet F a une image située à l'infini (2)
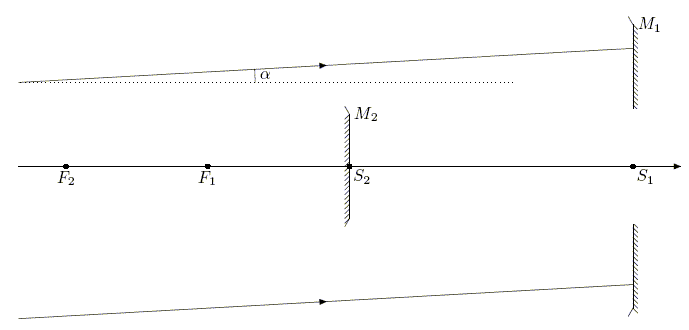
F et F' sont onfondus. M2. Le miroir M1 est
concave avec une ouverture à son sommet
S1 ; M2 est convexe, sa
face réfléchissante tournée vers
celle de M1. On observe à travers ce télescope
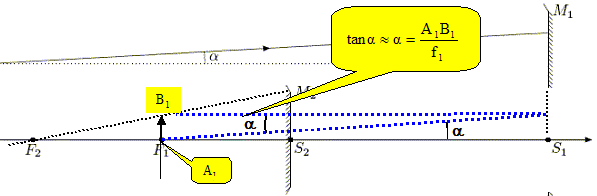
un objet AB dont l'extrémité A est
située sur l'axe optique. L'objet étant très
éloigné les rayons issus de B qui
atteignent le miroir M1 sont
quasiment parallèles et forment avec l'axe optique
l'angle a. Après
réflexion sur M1, ces rayons
se réfléchissent sur M2 et
forment une image finale A'B' située au
voisinage de S1.
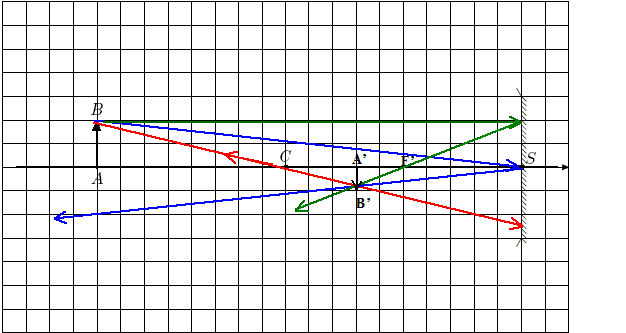
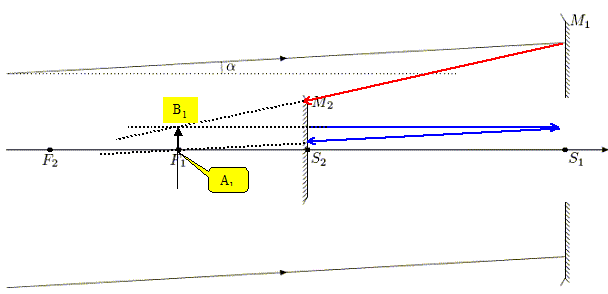
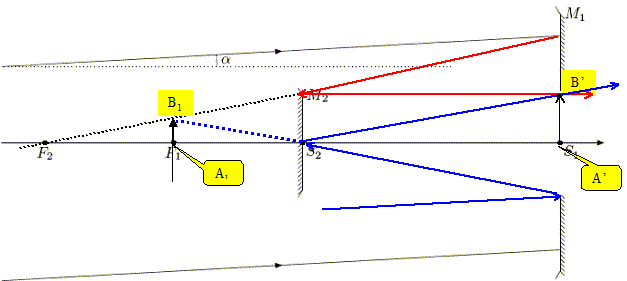
Effectuer les constructions géométriques des images intermédiaires A1B1 de AB par M1 et finale A'B'. L'objet AB étant à l'infini, l'image A1B1 est au foyer F1. Imaginer un rayon incident parallèle à l'axe optique : le rayon réfléchi sur M1 passe par F1 ( tracé bleu).
Le rayon incident passant par B1 passe par F2 : il se réfléchi sur M2 parallèlement à l'axe optique (tracé rouge).
On désigne par f1 et f2 les distances focales comptées positivement, des deux miroirs M1 et M2 (f1 = F1S1, f2 = F2S2 ) et par D = S2S1 la distance séparant les deux miroirs. Exprimer D en fonction de f1, f2 pour que l'image finale A'B' soit située dans le plan de S1. Simplifier cette expression lorsque f1 >> f2. F1 est le point objet ; son image donnée par M2 est S1.
réduire au même dénominateur, il vient : (D-f1)f2+Df2 = -D(D-f1) D2+(2f2 -f1 ) D -f1f2 =0 ; D = (2f2 -f1 )2+4f1f2 = 4f22 +f12. D= - ½(2f2 -f1 )+ ½[4f22 +f12]½. si f2<<f1, il vient : D =f1. Déterminer dans ces conditions, la taille de l'image intermédiaire A1B1 en fonction de a et f1.
En déduire celle de l'image finale A'B' en fonction de a, f1 et f2. Grandissement du miroir M2 :
Simplifier cette expression lorsque f1 >> f2. A'B' = f12a/f2. A.N : a= 10-3 rad, f1 = 40 cm et f1/f2 = 20. A'B' = 20*40/1000 =0,8 cm = 8 mm. A1B1 =f1a= 40/1000 =0,04 cm = 0,4 mm.
|
|||||||
|
|
|||||||
|
|