|
transformations irréversibles : entropie ; pompe à chaleur concours Mines 05 |
|||||||
|
|||||||
|
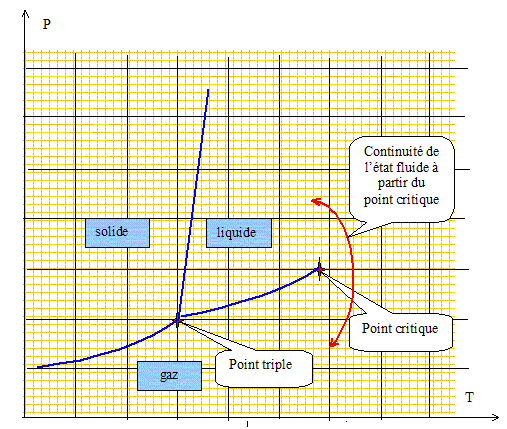
On donne les coordonnées du point triple (TT =217 K ; PT =510 kPa ) et du point critique (TC =304 K ; PC =73 MPa ) du dioxyde de carbone. Tracer une allure du diagramme (pression, température) pour le dioxyde de carbone, sans chercher à respecter des échelles. Expliquer à partir de ce diagramme ce qu'on appelle la continuite de l'état fluide. Quel est le phénomène observé au point critique ?
Lorsqu'on met au contact deux systèmes thermodynamiques séparément homogènes et à l'équilibre thermodynamique, on observe transitoirement une discontinuité des grandeurs intensives. Il en est ainsi lors de la detente de Joule Gay-Lussac et lors de la mise au contact de deux corps de températures différentes. On opère une détente de Joule Gay-Lussac pour une mole de gaz parfait monoatomique de volume initial V, et de température initiale T. Le volume final est V'=3V. Déterminer, en précisant soigneusement toutes les hypothèses et en détaillant tous les calculs, la variation d'entropie DS de cette transformation et commenter son signe. Système adiabatique : le transfert thermique Q est donc nul. Système indéformable : le travail des forces de pression W est nul en conséquence DU = 0 ; l'énergie interne est constante. Or l'énergie interne d'un gaz parfait ne dépend que de la température : donc T0=Tf. L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dS =dQ/T= (dU-dW)/T = Cv, m /T dT+ PdV/T = R/(g-1) /T dT+ RdV/V intégrer entre T0 et Tf : DS =Cv, m ln(Tf /T0) + Rln(Vf /V0) ; DS = Rln(Vf /V0) = Rln 3= 9,1 J K-1. Bilan entropique : entropie échangée Se1 = Q/T0 = 0 entropie créée
Sc1 = DS
- Se1
=9,1 J
K-1. La discontinuité de la pression est la source de l'irréversibilité. Dans une enceinte adiabatique, on met deux corps indéformables de même capacité calorifique (C ) au contact thermique ; leurs températures initiales respectives sont T1 et T2 et on attend l’équilibre thermique (température T). Déterminer la variation d’entropie de cette transformation et commenter son signe. Système adiabatique : le transfert thermique Q est donc nul. Système indéformable : le travail des forces de pression W est nul en conséquence DU = 0 ; l'énergie interne est constante. DU = DU1+DU2 =CDT1+CDT2 =0 d'où DT1 =- DT2 ; T-T1 = -(T-T2) d'où T = ½( T1 +T2). L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dS =dQ1/T1+dQ2/T2. Pour des phases condensées : dQ1=CdT1 et dQ21=CdT2 dS =C [dT1/T1+dT2/T2]= C[dlnT1+d lnT2] par intégration entre l'état initial et l'état final : DS = C ln (T/T1) + C ln (T/T2) = C ln (T2/(T1T2). DS = C ln[ ( T1 +T2)2 / (4T1T2). Si T1=T2, DS=0 ; si T1 différent de T2, ( T1 +T2)2 / (4T1T2) est supérieur à 1 : donc DS>0 entropie échangée Se =
0 ( adiabatique) entropie créée
Sc = DS
- Se
=DS, valeur
positive si T1
différent de T2. Ce résultat précédent est
conforme au second principe de la thermodynamique :
la transformation est irréversible,
l'entropie créée est positive. La discontinuité de la température
est la source de
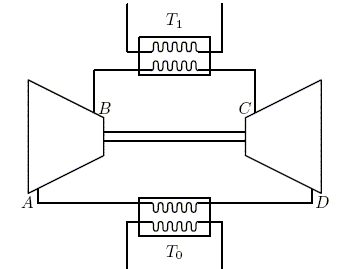
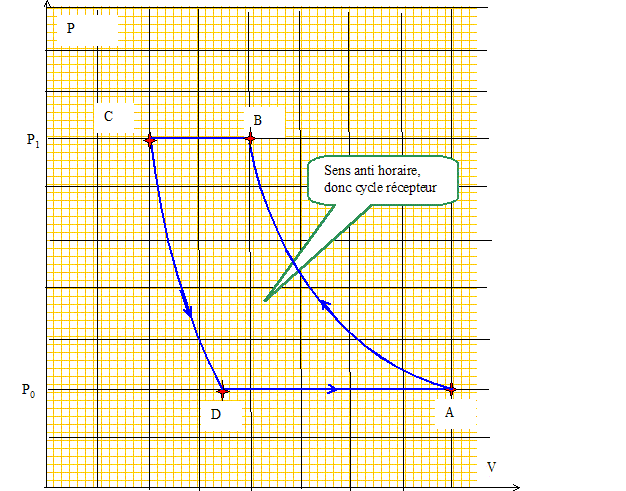
l'irréversibilité. Une pompe à chaleur effectue le cycle de Joule inversée suivant : . L'air pris dans l'état A de température T0 et de pression P0 est comprimé suivant une adiabatique quasi statique (ou réversible) jusqu'au point B où il atteint la pression P1. . Le gaz se refroidit à pression constante et atteint la température finale de la source chaude, T1, correspondant à l'état C. L'air est ensuite refroidi dans une turbine suivant une détente adiabatique quasi statique pour atteindre l'état D de pression P0. . Le gaz se réchauffe enfin à pression constante au contact de la source froide et retrouve son état initial A.
On considère l'air comme un gaz parfait de coefficient isentropique g = 1,4. On posera b= 1- g-1 et a = P1/P0. Pour les applications numLeriques, on prendra :T0 = 283 K(10 °C), T1 = 298 K(25°C) ; a = 5, R = 8,31 J K-1mol-1 (constante des gaz parfaits).
A-> B : adiabatique réversible. P01- g T0g = P11- g TBg TB =T0 [P0/P1] (1-g) /g = T0 [1/a]-b ; TB =T0 ab =283 * 50,285 = 448 K. C-> D : adiabatique réversible. P11- g T1g = P11- g TDg TD =T1 [P1/P0] (1-g) /g = T1 a-b ; TD =T1 a-b =298 * 5-0,285 = 188 K.
e = énergie prélevée à la source chaude / travail investi = -QBC/Wcycle. Montrer qu’elle s’exprime seulement en fonction de a et b. DUcycle =0 ; DUcycle =Wcycle+ QBC + QDA.(1) QAB= QCD=0 (adiabatiques) QBC = cP(TC-TB) = cP(T1-TB) ; QDA = cP(TA-TD) = cP(T0-TD). (2) (1) donne : e = QBC/(QBC + QDA) = 1/(1+QDA/QBC] (2) donne : QDA/QBC =(T0-TD) / (T1-TB) Or TB =T0 ab et TD =T1 a-b d'où : (T0-TD) / (T1-TB) =(T0-T1 a-b) / (T1-T0 ab ) = a-b (T0 ab-T1)/ (T1-T0 ab ) = -a-b par suite : e = 1/(1-a-b) Calculer sa valeur. e = 1/(1-5-0,285)=2,7. Quelles doivent être les transformations du fluide si on envisage de faire fonctionner la pompe à chaleur suivant un cycle de Carnot réversible entre les températures T0 et T1 ? Le cycle de Carnot compend deux adiabatiques réversibles et deux isothermes réversibles ( thermostas aux températures T0 et T1). Etablir l’expression de son efficacité eC. DUcycle =0 ; DUcycle =Wcycle+ QBC + QDA. La variation d'entropie est nulle sur le cycle réversible : QBC /T1 + QDA/T0 =0 QDA/QBC = -T0 /T1 et eC = 1/(1-T0 /T1). Calculer sa valeur. eC= 1 / (1-283/298) =19,9. Comparer les valeurs obtenues pour e et eC. Interpréter la différence observée. L'efficacité d'un cycle réversible (Carnot) est supérieure à celle d'un cycle irréversible (Joule).
Donner l’expression de l’entropie créée, si, pour une mole d'air mise en jeu dans le parcours du cycle de Joule inversé, en fonction de x = T0ab/T1, R et b. Sur le cycle la variation d'entropie est nulle DS=0. Or DS = Sé + Sc d'où : Sc = -Sé = -QBC /T1 - QDA/T0. Or QBC =cP(T1-TB) ; QDA = cP(T0-TD). et TB =T0 ab ; TD =T1 a-b Sc = -cP [1-T0/T1ab +1-T1 /T0a-b] = -cP [2-x-1/x] De plus cP=gR/(g-1) = R/b. Sc = R/b [x+1/x-2]. Etudier le signe de cette expression pour x positif ou nul. x+1/x-2 = (x2-2x+1 )/x =(x-1)2/x expression toujours positive si x >0 ; expression nulle si x=1. Calculer sa valeur. x= 283/298*50,285 =1,50 ;
Sc=8,31*1,4/0,4 *0,52/1,5 =
4,84 J K-1
mol-1.
La pompe à chaleur envisagée est utilisée pour chauffer une maison. Sachant qu'en régime permanent les fuites thermiques s'élèvent à Qf = 20 kW, calculer la puissance mécanique du couple compresseur-turbine qui permet de maintenir la maison à température constante. P = Qf/e = 20 / 2,7 = 7,4 kW.
|
|||||||
|
|
|||||||
|
|