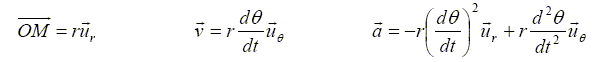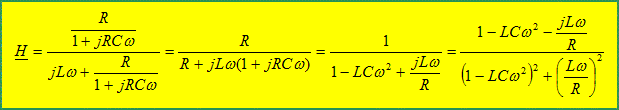|
continuité, discontinuité ; pendule simple, dipôle RLC, nombres complexes concours Mines 05 sans calculatrice. |
|||||||
|
|||||||
|
On rappelle qu’une fonction y=f(x) est une fonction continue en x0 si et seulement si la limite à gauche en x0 de f est égale à la limite à droite et à la valeur f(x0). Dans tout ce sujet, on notera x0- une valeur de x immédiatement inférieure à x0, x0+ une valeur de immédiatement supérieure à x. La continuité peut donc s’écrire aussi : f(x0-) =f(x0+)=f(x0). On rappelle les coordonnées dans la base polaire des vecteurs position OM, vitesse v et accélération a dans le cas du mouvement circulaire de rayon r :
On considère un mobile ponctuel de masse constante m soumis, dans un référentiel galiléen, à un ensemble de forces de résultante f, partout et constamment définie dans l’espace et le temps. En utilisant le principe fondamental de la dynamique (ou théorème du centre d’inertie), montrer que, sous cette hypothèse, la norme du vecteur vitesse du mobile est une fonction continue du temps. f = mdv/dt f
est "partout et constamment
définie" ; donc le vecteur vitesse est une fonction
dérivable par rapport au temps et en
conséquence la vitesse est une fonction continue.
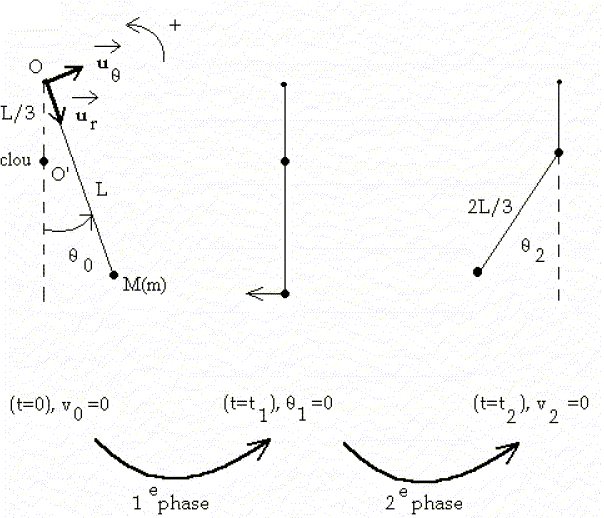
Un mobile ponctuel M de masse m, est accroché à l'extrémité d'un fil inextensible de longueur L et de masse negligeable, dont l'autre extrémité est fixe en O. On néglige tout frottement et on repère l'inclinaison q du brin de fil soutenant M par rapport à la verticale. Lorsque q>0, le système se comporte comme un pendule simple de centre O et de longueur de fil L. A la verticale et en dessous de O, un clou est plante en O' avec OO'=L/3, qui bloquera la partie haute du fil vers la gauche : quand q<0, le système se comporte donc comme un pendule simple de centre O' et de longueur de fil 2L/3. A la date t=0, on abandonne sans vitesse initiale le mobile M en donnant au fil une inclinaison initiale q0>0. On note t1 la date de la première rencontre du fil avec le clou, t2 la date de première annulation de la vitesse du mobile pour q<0. L'intervalle de dates [0,t1[ est nommé premiere phase du mouvement, l'intervalle ]t1, t2] est nommé deuxième phase. A la date t1- immédiatement inférieure à t1, le fil n'a pas encore touché le clou et à la date t1+ immédiatement supérieure, le fil vient de toucher le clou. Etablir l'équation différentielle vérifiée par q pour la première phase du mouvement.
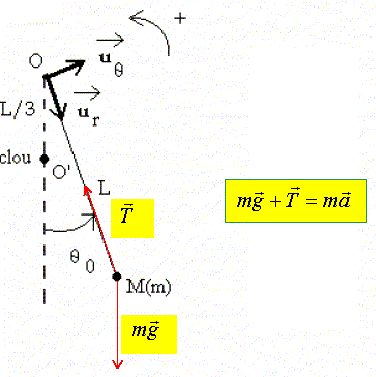
Sur ur : -T +mg cos q = -mL(dq/dt)2. Sur uq : -mg sin q = mL d2q/dt2. d'où l'équation différentielle : d2q/dt2 + g/L sin q =0. Dans l'hypothèse des petites oscillations, on suppose que sin q proche de q. Reconnaitre l'équation différentielle d'un certain type d'oscillateur et en déduire, sans résoudre l'équation, la durée dtI de la première phase du mouvement. oscillateur harmonique : d2q/dt2 + g/L q =0. w02 = g/L ; période T = 2p/w0=2p [L/g]½. La première phase du mouvement correspond à un demi-aller soit à un quart de période : dtI = 0,5p [L/g]½. En utilisant le théorème de l'énergie mécanique, déterminer la vitesse de M à la date t1-. L'énergie mécanique initiale est sous forme potentielle de pesanteur. On choisi l'origine de cette énergie au point le plus bas de la trajectoire de M. EM(0)= mgL(1- cosq0). L'énergie mécanique à la date t1- est sous forme cinétique : EM(t1- )= ½mv- 2. La tension T, perpendiculaire à la vitesse v, ne travaille pas ; le poids est une force conservative :donc, l'énergie mécanique se conserve. mgL(1- cosq0) = ½mv-2 ; v- =[ 2gL(1- cosq0)]½. En déduire la vitesse angulaire w1- =dq/dt à cette date. w1- = -v- /L = -[ 2g/L(1- cosq0)]½.
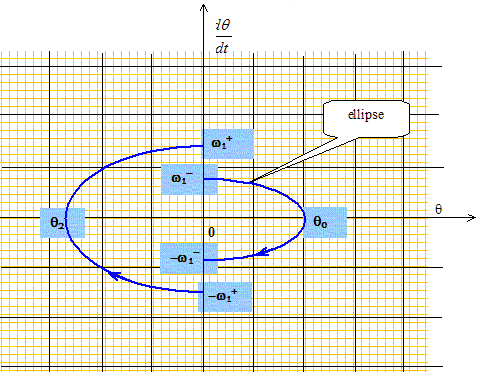
hypothèse : petites oscillations ; la période devient : T = 2p [2L/(3g)]½. La seconde phase du mouvement correspond à un demi-aller soit à un quart de période : dtII = 0,5p [2L/(3g)]½. Déterminer l'expression de l'angle q2 à la date t2. Ecrire la conservation de l'énergie mécanique : mgL(1- cosq0) = ½mv-2 =mg 2L/3(1- cosq2) 1- cosq0 = 2/3(1- cosq2) ; 1/3-cosq0 = -2/3cosq2 ; cosq2 = 1,5cosq0-0,5. Décrire brièvement la suite du mouvement de ce système et donner l’expression de sa période T. à t > t2, le pendule rebrousse chemin ; il repasse à la position d'équilibre avec la même vitesse qu'à l'aller ; il atteindra enfin la position q=q0 et on retrouvera la phase n°1, puis la phase n°2. période T = 2(dtI+dtII) =p [L/g]½+p [2L/(3g)]½. Dresser l’allure du portrait de phase, dans le système d’axes (q ; dq/dt). Conclure.
La modification brutale de la longueur du fil, entraîne une discontinuité de la vitesse angulaire.
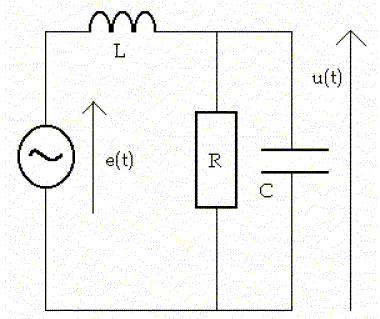
Un circuit électrique comprend un résistor de résistance R, une bobine d’inductance L et un condensateur de capacité C, toutes constantes. Expliquer pourquoi la tension aux bornes du condensateur et l’intensité du courant traversant la bobine sont des fonctions continues du temps. L'énergie électrique stockée dans un condensateur est une fonction continue. Or EC= ½Cu2C ; C étant une constante, alors uC est une fonction continue du temps. L'énergie électromagnétique stockée dans une bobine inductive est une fonction continue. Or EL= ½Li2 ; L étant une constante, alors i est une fonction continue du temps. On considère le circuit de la figure ci-dessous, alimenté par un générateur de tension alternative sinusoidale du type e(t) =E cos (wt) et on s'interèsse au régime sinusoidal forcé.
Etablir l’expression de la fonction de transfert complexe en boucle ouverte de ce circuit assimilé à un quadripôle : H= u / e. Admittance complexe de l'ensemble R C : Y1 = 1/R+jCw=(1+jRCw )/R Impédance complexe correspondante : Z1=R/(1+jRCw ) Impédance complexe du dipôle RLC: Z= jLw +Z1 H= Z1 / Z
En déduire la relation entre les grandeurs réelles e(t) et u(t) et et leurs éventuelles dérivées temporelles. e = u [1+LC (jw)2 +L/R jw] La dérivée première par rapport au temps correspond à la multiplication par jw. La dérivée seconde par rapport au temps correspond à la multiplication par (jw)2. d'où e(t) =u(t) + L/R du(t)/dt +LC d2u(t)/dt2.
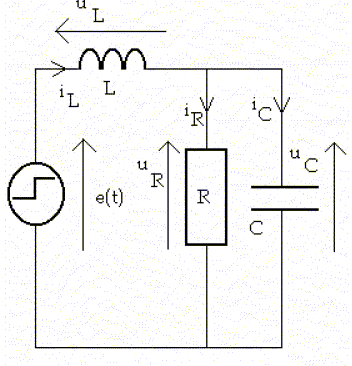
On considère maintenant le circuit de la figure ci-dessous, alimenté par un générateur d’échelon de tension dont la tension est : e(t)=0 pour t<0 et e(t)=E pour t>0.
A la date t0- , toutes les grandeurs électriques sont nulles : uL=uR=uC=0 et iL=iR=iC=0. On admettra pour la suite de cette partie que la tension aux bornes du condensateur vérifie l’équation différentielle : e(t) =uc + L/R duc dt +LC d2uc /dt2. Montrer que le type de régime dépend de la valeur de la résistance R, comparée à celle d'une résistance critique RC dont on donnera l’expression. L’observation d’oscillations amorties a-t-elle lieu pour R>RC ou pour R<RC ? Interpréter physiquement. équation caractéristique associée à : uc + L/R duc dt +LC d2uc /dt2 =0 LC r2 +L/R r +1 =0 ; D= (L/R)2-4LC Le discriminant est nul si R prend la valeur RC=2(L/C)½. Si R<RC, alors D>0, régime apériodique. Si R>RC, alors D<0, régime pseudopériodique ( amortissement). Pour de grande valeur de R, l'intensité iR est très faible et le circuit se comporte comme un dipôle LC. Donner en les justifiant les valeurs des six grandeurs électriques uL, uR, uC, iL, iR et iC à la date t0+. uC =q/C=0, le condensateur ne se charge pas instantanément. uR=uC=R iR =0 : donc iR=0. uC+uL= E ; uC=0 par suite uL= E. Continuité de l'intensité iL : iL(t0-) = iL(t0+) =0 additivité des intensités ( loi des noeuds) : iL= iR+ iC =0 ; iR=0 donc iC =0
Quelles sont dans ce cas les grandeurs électriques (capacité, charge, tension, énergie électrique) encore continues et par quels coefficients respectifs sont multipliées les autres ? Justifier quantitativement et interpréter physiquement les réponses. La capacité est inversement proportionnelle à l'épaisseur e : si e est divisée par 2, alors la capacité C double. La charge du condensateur ne se fait pas instantanément : la charge q est une grandeur continue. Or uC=q/C ; si C double alors uC est divisée par deux. ( discontinuité de uC ). Energie stockée par le condensateur : ½ q2/C ; C double et la charge q est constante, donc l'énergie est divisée par deux. ( discontinuité de l'énergie) La diminution de l'énergie est due au travail positif de la force électrique attractive existant entre les plaques lors de leur, rapprochement. |
|||||||
|
|
|||||||
|
|