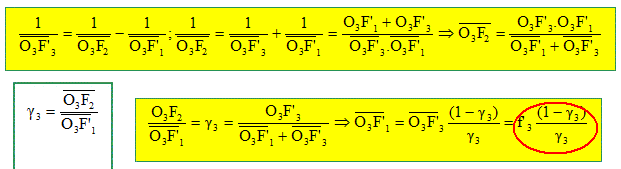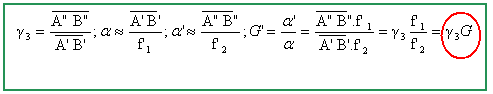lunette astronomique : grossissement concours Mines 04

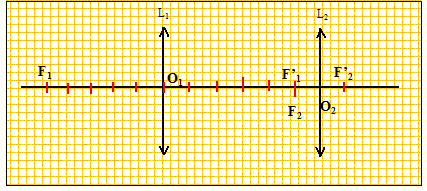
On considère une lunette astronomique formée :

. d'un objectif constitué d'une lentille mince convergente de distance focale f'₁=O₁F'₁>0.

. d'un oculaire constitué d'une lentille mince convergente de distance focale f'₂=O₂F'₂>0.

Ces deux lentilles ont même axe optique D.

On rappelle qu'un oeil normal voit un objet sans accommoder quand celui-ci est placé à l'infini.

On souhaite observer la planéte Mars, qui est vue à l'oeil nu sous un diamètre apparent a.

Pour voir la planète nette à travers la lunette, on forme un système afocal.

Que cela signifie-t-il ? Que cela implique-t-il pour les positions des lentilles ?

L'image définitive est à l'infini.

L'image intermédiaire donnée par l'objectif ( servant d'objet pour l'oculaire ), se trouve au foyer objet F₂ de l'oculaire.

L'objet étant à l'infini, l'image intermédiaire se trouve au foyer image F'₁ de l'objectif.

F'₁ et F₂ sont donc confondus.

Faire le schéma de la lunette en prenant f'₁ =5f'₂.

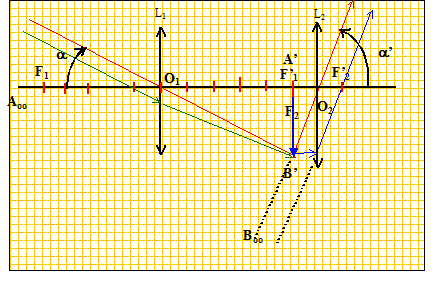
Dessiner sur ce schéma la marche à travers la lunette d'un faisceau lumineux formé de rayons issus de l'étoile.

On appellera A'B', l'image intermédiaire.  

On souhaite photographier cette planète. Où faut-il placer la pellicule ?

Dans le plan focal image de l'objectif, sur lequel se forme A'B'.

On note a', l'angle que forment les rayons émergents extrèmes en sortie de la lunette.

L'image est-elle droite ou renversée ?

 L'image définitive est renversée.

La lunette est caractérisée par son grossissement G= a'/ a .

Exprimer G en fonction de f'₁et f'₂.

tan a = A'B'/O₁F₁ = A'B'/ f'₁ proche de a radian si l'angle est petit.

tan a' = A'B' /f'₂ proche de a' radian si l'angle est petit.

a et a ' sont de sens contraire donc le grossissement G est négatif : G = - f'₁ /f'₂.

Le principal défaut d'une lentille est appelé défaut d'aberrations chromatiques : expliquer brièvement l'origine de ce défaut et ses conséquences. Le verre constituant les lentilles est un milieu dispersif pour la lumière blanche. L'image d'un point est une petite tache irrisée de rouge ou de bleu. Pour quelle raison un miroir n'a-t-il pas ce défaut ? La lumière blanche suit le phénomène de réflexion ; la lumière ne change pas de milieu. L'air n'est pas un milieu dispersif.

On veut augmenter le grossissement de cette lunette et redresser l’image

Pour cela, on interpose entre L₁et L₂, une lentille convergente de distance focale f'₃=O₃F'₃ >0.

L’oculaire est déplacé pour avoir de la planète une image nette à l’infini à travers le nouvel ensemble optique.

Quel couple de points doit conjuguer L₃ pour qu’il en soit ainsi ?  

 F'₁ et F₂.

On appelle g₃, le grandissement de la lentille L₃.

En déduire O₃F'₁ en fonction de O₃F'₃ et g₃.

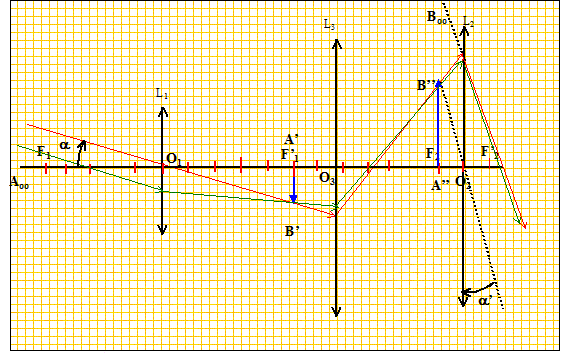
Faire un schéma.

(On placera O₃ entre F'₁ et F_2, et on appellera A'B' la première image intermediaire et A"B", la seconde image intermédiaire).

En déduire le nouveau grossissement G' en fonction de g₃ et G. Comparer à G, en norme et en signe.  

g₃ et G sont négatifs : G' est positif ( l'image définitive est droite ).

G' est plus grand que G.