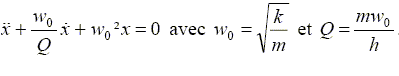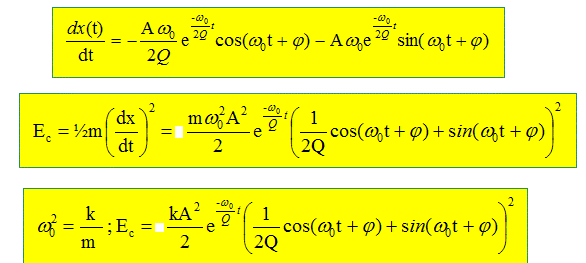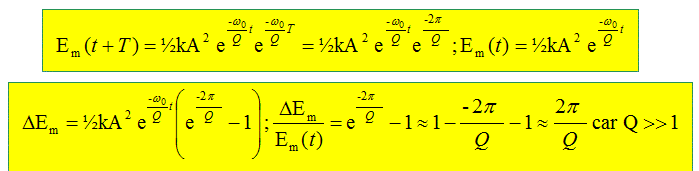facteur de qualité : étude d'un oscillateur amorti concours Mines 04

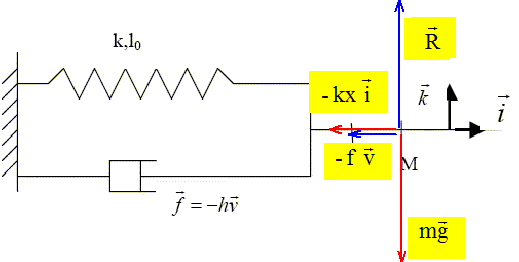
On considère le dispositif mécanique suivant, placé dans le référentiel R du laboratoire, supposé galiléen.

Il est composé d’une bille M, supposée ponctuelle, de masse m qui glisse sans frottement sur un axe horizontal. Elle est reliée :

• à un ressort de raideur k et de longueur à vide l₀, maintenu fixé à une de ses extrémités à un mur vertical.

• à un dispositif « amortisseur » fixé au même mur, qui soumet la bille à une force de frottement de type fluide   f = -h v.

On note O, la position de la bille quand le ressort est à sa longueur à vide, et en prenant O comme origine, on repère la position de M par x= mesure algébrique de OM.

Faire un bilan des forces et justifier très brièvement que le système n’est pas conservatif.

La force de frottement fluide n'est pas conservative : l'énergie mécanique va diminuer.

En appliquant le théorème de l’énergie cinétique à la bille, montrer que la variation de l’énergie mécanique s’écrit sous la forme :

dE_m= -hv²dt.

Entre les instants t et t +dt :

Le poids et l'action du support, perpendiculaires à la vitesse, ne travaillent pas. La puissance de ces forces est nulle.

Travail de la force de rappel : -kxdx ; puissance : -kxdx/dt.

Travail de la force de frottement fluide : -fv dx avex dx=vdt soit -fv²dt ; puissance : -fv²

Théorème de l'énergie cinétique : dE_c/dt = -kx dx/dt -fv².

or kx dx = d_{Epotentielle élastique} = dE_p, d'où : dE_c/dt + dE_p/dt = -fv² ; d(E_c+E_p)/dt = dE_M/dt.

dE_M/dt = -fv².

Appliquer le Principe Fondamental de la Dynamique à la bille dans R, et montrer que :

Sur l'axe des abscisses : -kx- hv = md²x/dt² avec v = dx/dt.

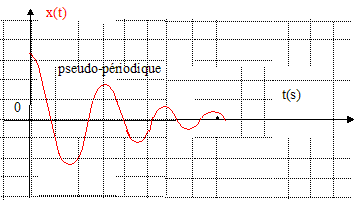
d²x/dt² + h/m dx/dt + k/m x = 0

 On pose w₀² = k/m ; Q= mw₀/h soit h/m = w₀/Q.

d'où : d²x/dt² + w₀/Q dx/dt +w₀² x =0. (1)

On se place dans le cas du régime pseudo-périodique. Les solutions sont de la forme :

Donner la condition sur Q pour être dans un tel régime.

Equation caractéristique liée à (1) :

r² + w₀/Q r +w₀² =0. Discriminant D = (w₀/Q)²-4w₀².

Le discriminant est négatif dans le cas du régime pseudo-périodique.(w₀/Q)²-4w₀² <0 soit Q >0,5.

Tracer l’allure de x(t).

On se place dans le cas de l'amortissement faible Q >>1.

Exprimer |DT/T₀|= |(T-T₀)/T₀| en fonction de Q et en déduire que w proche w₀.

w=w₀[1-1/(4Q²)]^½ ; w₀ = 2p/T₀ ; w = 2p/T ; w /w₀ =T/T₀ = [1-1/(4Q²)]^½ ;

|(T-T₀)/T₀| = | [1-1/(4Q²)]^½ -1|

Or si Q<<1, [1-1/(4Q²)]^½ voisin de 1-1/(8Q²)] et | [1-1/(4Q²)]^½ -1| proche de 1/(8Q²)

|DT/T₀|= 1/(8Q²).

Si Q >>1, alors DTproche de 0, T proche deT₀ et w proche de w₀.

Interprétation énergétique du facteur de qualité Q.

On suppose w =w₀.

Justifier que l’énergie potentielle de M peut s’écrire E_p(t) =½kx²(t), puis expliciter E_p(t).

Travail de la force de rappel : dW= -kx dx

Expliciter E_c(t), l’énergie cinétique de M en fonction du temps.

Montrer que l’énergie mécanique E_m(t) est de la forme E_c(t) = K₁exp(-K₂t) où l’on exprimera K₁ en fonction de A et k , et K₂ en fonction de w₀ et Q.

Montrer que Q = 2pE_m(t) /DE_m(t).