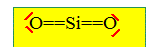propriétés chimiques de la silice ; cinétique d'ordre 1 : loi d'Arrhénius concours Mines 04

Structure :

Ecrire la configuration électronique dans l’état fondamental du silicium de numéro atomique Z=14. Citer un élément de la même colonne.

1s² 2s² 2p⁶ 3s² 3p² ; éléments carbone, germanium.

Le silicium existe à l’état naturel sous les trois formes isotopiques suivantes :

²⁸₁₄Si : 92,2 % ; ²⁹₁₄Si : 4,7 % ; ³⁰₁₄Si : 3,1 % ;

Estimer la masse molaire atomique moyenne de l'élément Si.

M= 28*0,922 + 29*0,047+30*0,031 = 28,1 g/mol.

La masse molaire de l’oxygène étant de 16 g/mol,

quelle est la masse molaire moyenne de la silice SiO₂ ?

28,1 + 32 = 60,1 g/mol.

On rappelle que le numéro atomique de l’oxygène est Z=8.

Proposer alors un schéma de Lewis de la molécule SiO₂. Quelle est la géométrie de cette molécule ? Citer une molécule de géométrie analogue à celle de SiO₂.

Si : 4 électrons de valence ; O : 6 électrons de valence.

type AX₂, linéaire comme CO₂.

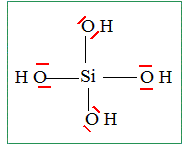
On trouve de la silice minérale sous forme, par exemple, d’anorthite de formule chimique CaAl₂Si₂O₈. L’altération de cette silice minérale par l’acide carbonique (CO₂ dissous formant l’acide H₂CO₃), présent dans les eaux de pluie, souterraines et fluviales, libère de la silice dissoute, que l’on notera DSi dont la formule chimique est H₄SiO₄. La réaction de dissolution est la suivante :

 CaAl₂Si₂O₈+ xH₂CO₃ + yH₂O = 2Al(OH)₃ + Ca²⁺ + a H₄SiO₄ + b HCO₃^-.

Proposer une formule de Lewis de la silice dissoute DSi.

Equilibrer cette réaction.    CaAl2Si2O8+ 2 H2CO3 + 6 H2O = 2Al(OH)3 + Ca2+ + 2 H4SiO4 + 2 HCO3-.

On va s’intéresser maintenant à la dissolution de la silice pure amorphe SiO₂ (s). La solubilité de cette silice dans l’eau est caractérisée par l’équilibre suivant où l’on retrouve alors la forme dissoute de la silice (DSi ou H₄SiO₄) :

(1) SiO₂ (s) + 2H₂O = H₄SiO₄ ; K₁ = 10^-2,7 à 25°C.

Calculer, à l’équilibre, la concentration en DSi à 25°C ?

K₁ =[H₄SiO₄] = 10^-2,7 =2,0 10^-3 mol/L.

En déduire la masse maximale de silice pure amorphe que l’on peut dissoudre dans un volume de 1 L d’eau pure.

2,0 10^-3*M(SiO₂) =  2,0 10^-3*60,1 = 0,12 g/L.

Propriétés acido-basiques de la silice : En fait, la solubilité de la silice varie en fonction du pH par suite des propriétés acides de DSi. Les équilibres acido-basiques mis en jeu sont les suivants : (2) H4SiO4 +H2O = H3SiO4- +H3O+ pK2 = 9,5 à 25°C (3) H3SiO4- +H2O = H2SiO42- +H3O+ pK3 = 12,6 à 25°C

Tracer le diagramme de prédominance des différentes espèces acido-basiques de la silice dissoute DSi.

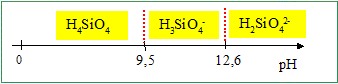
Sachant que le pH des eaux naturelles est généralement compris entre 7 et 8, quelle est la forme prédominante en solution de la silice ?

à pH < 9,5 , la forme H₄SiO₄ prédomine.

Pour une eau dont le pH est compris entre 10 et 12,

écrire l’équation bilan de dissolution de la silice (en milieu basique).

Calculer la constante K'₂ de cet équilibre en fonction de K₁, K₂ et K_e (produit ionique de l’eau).

H₃SiO₄^- prédomine dans ce domaine de pH.

SiO₂ (s) + H₂O + HO^- = H₃SiO₄^- ;

K'₂ = [H₃SiO₄^-] / [HO^-] ;

Or : K₂ =[H₃SiO₄^-][H₃O⁺] / [H₄SiO₄] et K₁ =[H₄SiO₄]

K'₂ = K₂ [H₄SiO₄]/ ( [HO^-][H₃O⁺]) ; K'₂ = K₂K₁ /K_e.

K'₂ = 10^-9,5 . 10^-2,7 / 10^-14 =10^+1,8 =63.

Pour une eau dont le pH est compris entre 13 et 14,

écrire l’équation bilan de dissolution de la silice (en milieu basique). Calculer la constante K'₃ de cet équilibre en fonction de K₁, K₂, K₃ et K_e.

H₂SiO₄^2- prédomine dans ce domaine de pH.

SiO₂ (s) + 2HO^- = H₂SiO₄^2- ;

K'₃ = [H₂SiO₄^2-] / [HO^-]² ;

Or : K₂ =[H₃SiO₄^-][H₃O⁺] / [H₄SiO₄] ; K₁ =[H₄SiO₄]

et K₃ =[H₂SiO₄^2-][H₃O⁺] / [H₃SiO₄^-]

K₂K₃ =[H₃O⁺]²[H₂SiO₄^2-]/ [H₄SiO₄]

K'₃ = K₂ K₃ [H₄SiO₄]/ ( [HO^-]²[H₃O⁺]²) ; K'₃ = K₃ K₂K₁ /K_e².

K'₃ = 10^-12,6.10^-9,5 . 10^-2,7 / 10^-28 =10^3,2 =1,6 10³.

Cinétique de dissolution de la silice biogénique dans l’eau :

La silice peut être incorporée par des organismes vivants, comme les diatomées ou les radiolaires. On parle alors de silice biogénique, SiO₂ ou BSi. Des études récentes ont montré que cette silice, d’origine semi-aquatique ou même terrestre, pouvait avoir un rôle important dans les cycles biogéochimiques. Quand la silice est incorporée dans les plantes, on parle de phytolithes. Ces phytolithes s’accumulent dans les estuaires des fleuves. On se propose d’étudier la cinétique de dissolution des phytolithes dans l’eau des fleuves.

 Pour étudier la dissolution en laboratoire, on place une certaine quantité initiale n_B0=10^-3 mol de silice biogénique, dans un volume V₀ =1 L d’eau. La silice biogénique se présente sous la forme de microcristaux que l’on suppose répartis de manière uniforme dans l’eau. On définit alors à l’instant t une concentration en silice biogénique par le rapport n_B(t)/V₀. L’expérience est réalisée à 60°C, en bain-marie agitant, avec adjonction de chlorure de sodium à 0,7 mol/L et en présence d’un tampon à pH=8. La silice biogénique va se dissoudre pour former de la silice DSi (H₄SiO₄) que l’on sait doser au cours du temps. L’équation de dissolution est : BSi + 2 H₂O = DSi.

Pourquoi utilise-t-on un tampon à pH=8 ici ?

H₄SiO₄ est la forme prédominante à pH =8. De plus, le pH des eaux naturelles est proche de 8.

Pourquoi l’expérience est réalisée à une température de 60°C alors que dans les conditions naturelles, les eaux sont à moins de 20°C ?

La température est un facteur cinétique : à 60°C, la vitesse de la réaction de dissolution est beaucoup plus grande qu'à 20 °C.

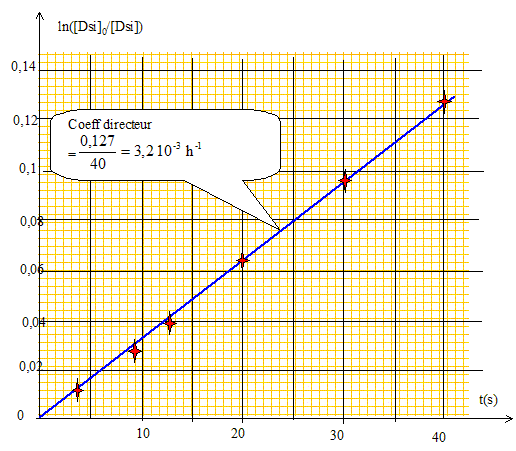
On appellera k la constante de vitesse.

BSi + 2 H₂O = DSi.

v = -d[BSi]/dt = k[BSi] ; d[BSi]/ [BSi] = -k dt ; d ln[BSi] = -k dt

Intégrer entre t=0 et t : ln[BSi] -ln [BSi]₀ = -kt ;

[BSi] = [BSi]₀ exp(-kt).

[DSi] = [BSi]₀ -[BSi] =n_B0/V₀(1-exp(-kt).

Quelle courbe faut-il tracer en fonction du temps pour vérifier l’hypothèse d’un ordre 1 ?

ln ( [BSi]₀ /[BSi] )= f(t), droite de coefficient directeur k.

Par une régression linéaire ou par une méthode graphique, vérifier que la cinétique est bien d’ordre 1. En déduire la valeur de k.

[DSi] mmol/L	0,014	0,026	0,040	0,066	0,097	0,127	0,156	0,184
t(heure)	4	8	12	20	30	40	50	60
[BSi] =[BSi]0 -[DSi] mmol/L	1-0,014 =0,986	1-0,026 =0,974	1-0,04=0,96	1-0,066 =0,934	1-0,097 =0,903	1-0,127=0,873	1-0,156=0,844	1-0,184=0,816
ln([BSi]0 /[BSi])	0,014	0,026	0,041	0,068	0,102	0,136	0,170	0,203

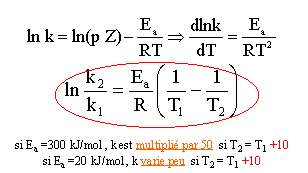
Dans l’hypothèse où k suit la loi d’Arrhénius, exprimer la constante de vitesse k₂ à la température T₂ en fonction de la constante de vitesse k₁ à la températureT₁.

Calculer alors numériquement la constante de vitesse de la dissolution à température de 20°C.

T₁ = 293 K ; T₂ = 333 K ; k₂ = 3,2 10^-3 h^-1 ; E_a=6 10⁴ Jmol^-1

ln(k₂/k₁) = 6 10⁴/8,314 [1/293-1/333]= 2,98 ;

k₂/k₁ = e^2,98 = 19,7 ; k₁ = k₂ /19,7 = 3,2 10^-3 /19,7 =1,6 10^-4 h^-1 ;

On donne l’énergie d’activation E_a=60 kJmol^-1 ; R= 8,314 S.I la constante des gaz parfaits . Conclure.

A 20 °C, la réaction est 20 fois plus lente qu'à 60°C : à 20 °C, l'expérience aurait durée plus d'un mois.