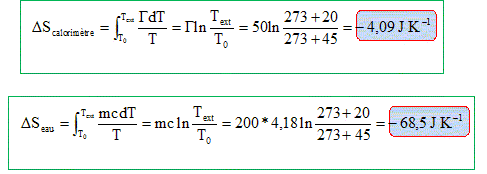Transitoires thermiques et électriques Mines 2002.

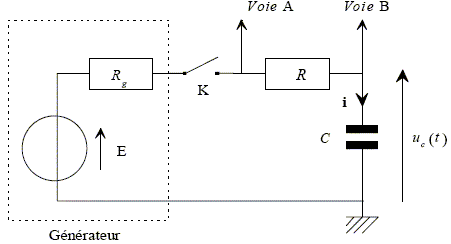
Transitoire électrique : Un dipôle comporte entre ses bornes un résistor de résistance R et un condensateur de capacité C placés en série. On le place aux bornes d'un générateur de force électromotrice E et de résistance interne Rg en série avec un interrupteur K . Initialement, le circuit est ouvert et le condensateur déchargé. Soit, uC la tension aux bornes du condensateur. A l'instant t=0, on ferme l'interrupteur, K . Determiner, sans calcul et en le justifiant uC(0+), i(0+). Continuité de la tension aux bornes du condensateur ou conservation de l'énergie : juste après la fermeture de K, le condensateur n'a pas encore eu le temps de se charger : uC(0+) = uC(0) = 0. Additivité des tensions : E = uC(0+) + (R+Rg)i(0+). uC(0+) =0 d'où : i(0+) = E/R. Etablir l'équation différentielle à laquelle obéit uC(t) . Additivité des tensions : E = uC(t) + (R+Rg) i(t). Or q(t) = C uC(t) et i(t) = dq(t)/dt d'où : i(t) = CduC(t) /dt. E = uC(t) + (R+Rg) C duC(t) /dt ; duC(t) /dt + 1/((R+Rg)C) uC(t) =+E/((R+Rg)C). u'C+1/t uC =E/t (1) Déterminer la constante de temps t du circuit, et donner son interpretation physique. t = (R+Rg)C. Au bout d'une durée supérieure à 5 t, le régime permanent est atteint : condensateur chargé. Etablir l'expression de uC(t). Solution générale de l'équation différentielle sans second membre u'C+1/t uC=0 uC=A exp(-t/t) avec A une constante Solution particulière de (1), régime permanent : uC(t) = E. Solution générale de (1) : uC=A exp(-t/t) +E On détermine A grâce aux conditions initiales uC(0)=0 soit : 0=A +E ; A=E. uC=E(1- exp(-t/t). Déterminer l'expression de t1 pour que uC=0,9E. uC(t1) = 0,9 E = E (1-exp(-t1/t)) ; 0,9 = 1-exp(-t1/t) ; exp(-t1/t) = 0,1. -t1/t = ln 0,1 ; t1= t ln 10. Dans l'étude expérimentale du circuit RC, on observe l'oscillogramme ci-dessous en utilisant un générateur délivrant des signaux créneaux. Les sensibilités sont : 1V/carreau vertical ; 0,1 ms/carreau horizontal . On néglige les caractéristiques de l'oscilloscope. 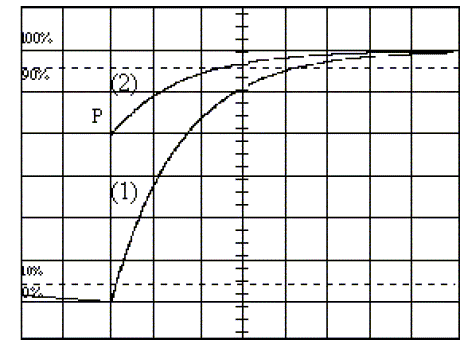Identifier les courbes (1) et (2) aux voies A et B en justifiant votre choix. D'après les branchements de l'oscilloscope, on visualise voie A, la tension aux bornes du générateur et voie B la tension aux bornes du condensateur. Or uC(t) est une fonction exponentielle croissante de 0 à E : (1) correspond à uC(t). De plus on constate la continuité de la courbe (1). Doit-on être sur le couplage alternatif AC ou le couplage continu DC ? DC : on travaille avec un générateur de tension continue. Preciser l'expression de la tension au point P. Sachant que R =100 W, déterminer Rg . Tension aux bornes du générateur à t=0+. Le condensateur est déchargé : uC(0+)=0 et i(0+) = E/(R+Rg). Tension aux bornes du générateur : E - Rgi(0+) =E[ 1- Rg/(R+Rg)] VP=E R / (R+Rg). VP= 2/3 E ( lecture graphe) ; 2/3(R+Rg) = R ; Rg = 0,5 R = 50 W. En déduire la valeur de C et E. 1V/carreau vertical : E = 6 V. Durée de la charge du condensateur : ~ 8 carreaux soit 0,8 ms 5 t ~ 8 10-4 s ; t ~ 1,6 10-4 s. t = (R+Rg) C ; C ~ 1,6 10-4 /150 = 1,1 10-6 F. Estimer une majoration de la fréquence du signal carré utilisé. Pour observer la charge complète il faut que la période du signal carré soit supérieure à 5 t soit 8 10-4 s. fréquence inférieure à 1/8 10-4 soit f <1250 Hz. Pour observer une charge et décharge complètes : f < 625 Hz. Comment pourrait-on observer l'intensité ? La tension uR aux bornes d'un conducteur ohmique et l'intensité qui le traverse sont proportionnelles : l'image de uR est l'image de l'intensité au facteur R près. Permutter R et C : on observe alors voie B, l'image de l'intensité. Transitoire thermique. On donne : m= 200 g ; c= 4,18 J K-1 g-1 ; G = 50 J/K; On rappelle que T(K)=T(°C)+273,15. Dans un calorimètre de capacite thermique G à la température extérieure, Text , on verse une masse m d'eau à la température extérieure, Text et on plonge une résistance chauffante de valeur R , alimentée sous une tension continue U. On considèrera comme système {eau-calorimètre} On note T la température, t le temps et c la capacité thermique massique de l'eau. On admet de plus que les fuites thermiques peuvent se traduire par une puissance de perte pext=k (T-Text). A quelle variation de fonction d'état s'identifie dQ ? A une pression constante, d Q correspond à la fonction d'état enthalpie dH. Faire un bilan d'énergie pendant un intervalle de temps dt. Montrer que dT/dt +T/t =TM/t. Energie gagnée par l'eau et le calorimètre : d Q = (mc+G) dT Energie perdue vers l'extérieur : pext dt=k (T-Text)dt Energie fournie par la résistance chauffante R : UIdt = U2dt/R. 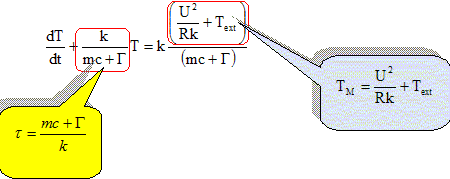Bilan : U2/R dt = (mc+G) dT +k (T-Text)dt Quelle est l'interprétation physique de TM ? Température en régime permanent : la puissance Joule compense, à chaque instant, la puissance perdue vers l'extérieur. On coupe le chauffage. On négligera la capacité thermique de la résistance chauffante. Refaire un bilan d'énergie pendant un intervalle de temps dt. En déduire T(t) . On notera T0=T , la température à l'instant t=0. Energie cédée par l'eau et le calorimètre : d Q = - (mc+G) dT Energie perdue vers l'extérieur : pext dt=k (T-Text)dt Bilan : -(mc+G) dT = k (T-Text)dt dT/ dt + kT / (mc+G) = kText/ (mc+G). dT/dt + T/t = Text/ t. (2) Solution générale de l'équation différentielle sans second membre T'+T/t=0 T=A exp(-t/t) avec A une constante Solution particulière de (2), régime permanent : T = Text. Solution générale de (2) : T=Aexp(-t/t) +Text. On détermine A grâce aux conditions initiales soit : T0=A +Text ; A=T0-Text. T=(T0-Text)exp(-t/t) +Text ; T=Text(1-exp(-t/t) )+T0exp(-t/t). On enregistre grâce à une interface la température T(t) au cours du refroidissement. Déterminer sur l'enregistrement t et Text. En déduire k. 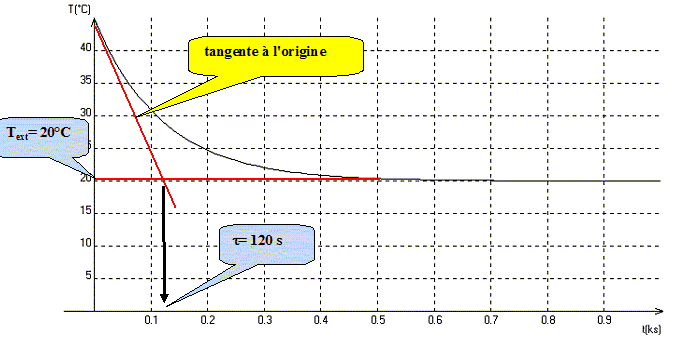k = (mc+G)/t = (200*4,18+50)/120 =7,38 W K-1. En déduire, littéralement puis numériquement entre les instants initial et final : la variation d'entropie pour le calorimètre DScalorimètre. la variation d'entropie pour l'eau DSeau. 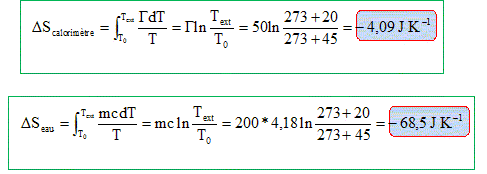l'entropie échangée Séchange. (mc+G) ( Text-T0) / Text = (200*4,18+50)*(-25) /293 = -75,6 J K-1. l'entropie créée Scréee. DS =Séchange+ Scréee ; Scréee =-4,09-68,5+75,6 = 3,0 J K-1. Conclusion. Scréee étant positive, la transformation est irréversible.

retour -menu