Médecine et mécanique des fluides : le système artériel.

On modèlise le système sanguin par un système artériel suivi d'un système capillaire. On considèrera que le sang est un liquide incompressible. Le système artériel. Le diamètre des artères est assez grand, et on considère qu'il n'y a pas de pertes de pression dans le système artériel ( résistance hydrodynamique nulle ). La pression Pa y est partout la même. Les artères sont élastiques, leur volume Va(t) est donc variable. La variation de Va est linéaire à la variation de pression. Leur différentielle obéit donc à l'équation : dVa(t) = C dPa(t) (1) où C est la capacitance ( indépendante du temps). Plus C est grand, plus le système artériel est élastique. Le système capillaire. On considère que les capillaires ne sont pas élastiques. Ils opposent par contre une résistance hydrodynamique Rh à l'écoulement du sang. La perte de pression entre l'entrée et la sortie du système capillaire est donc : DP(t) = Rh Q(t) (2) où Q(t) est le débit du sang dans le système capillaire. On considère que la pression à la sortie du système capillaire est nulle. Soit QC(t) le débit à l'entrée du système artériel, et QS(t) le débit à la sortie du système artériel. En partant du volume dVa gagné par le système artériel entre t et t+dt, montrer que l'équation différentielle reliant QS(t) et QC(t) est : RhC QS(t) dt +QS(t) =QC(t) Le débit volumique n'est pas conservé dans les artères : entre les dates t et t+dt , sa variation peut s'écrire : QC(t) + dVa dt =QS(t) Soit en tenant compte de (1) : QC(t) + CdPa dt =QS(t) (3) La variation de pression DP(t) dans le système capillaire s'écrit : pression à la sortie (nulle) - pression à l'entrée Pa(t). DP(t) = 0- Pa(t) = Rh Q(t) d'après (2) ; repport dans (3) : QC(t) + -CRhdQ dt =QS(t) Or le débit à la sortie du système artériel est égal au débit à l'entrée du système vasculaire d'où Q(t) = QS(t). 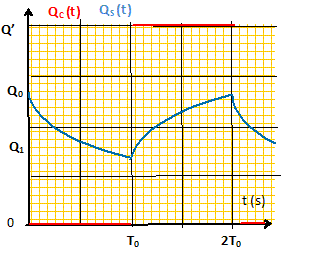QC(t) = CRhdQS dt +QS(t) Le coeur se trouve à l'entrée du système artériel. Le coeur est une pompe qui injecte du sang dans le système artériel pendant une partie du cycle cardiaque ( systole), puis se ferme et n'injecte plus rien ( diastole). La diastole et la systole se succèdent et dure chacune un temps T0. Pendant la diastole, on a donc QC(t) = 0. Déterminer QSd(t) avec pour condition initiale QS(0) = Q0. Solution générale de l'équation différentielle sans second membre : QS(t) = A exp(-t/t) en posant t = CRh et A une constante. Solution particulière de l'équation différentielle complète : QSd(t) = QC(t) = 0. Solution générale de l'équation différentielle complète : QSd(t) = A exp(-t/t) + 0. A t=0 : QSd(0) = A = Q0. QSd(t) = Q0 exp(-t/t). Pendant la systole, le coeur injecte du sang dans le système artériel, avec un débit constant Q'. On a donc QC(t) = Q'. Déterminer QSS(t). Solution générale de l'équation différentielle sans second membre : QS(t) = B exp(-t/t) en posant t = CRh et B une constante. Solution particulière de l'équation différentielle complète : QSS(t) = QC(t) =Q'. Solution générale de l'équation différentielle complète : QSS(t) = B exp(-t/t) + Q'. A t=T0 : QSS(T0) = B exp(-T0/t)+ Q' ; Il y a continuité du débit à la sortie du système artériel, soit : QSd(T0) =QSS(T0) = Q1. B exp(-T0/t)+ Q' = Q0 exp(-T0/t) = Q1 d'où B = [Q1- Q']exp(T0/t)=[Q1- Q'] Q0/Q1 =Q0-Q' Q0/Q1 = Q0(1-Q' /Q1). QSS(t) = Q0(1-Q' /Q1) exp(-t/t) + Q'. En écrivant la continuité du débit à la sortie du système artériel à t = 2 T0, déduire l'expression de Q0 en fonction de Q', T, R et C. Comparer Q0 et Q'. QSS(2 T0) = Q0(1-Q' /Q1) exp(-2 T0/t) + Q' et de plus QSS(2 T0) =Q0. Q0(1-Q' /Q1) exp(-2 T0/t) + Q'=Q0. Or Q1 = Q0exp(-T0/t) d'où : Q0 exp(-2 T0/t) -Q'exp(-T0/t) + Q' =Q0. Q0[1-exp(-2 T0/t) ] = Q'[1-exp(-T0/t)]. Q0= Q' [1-exp(-T0/t)] [1-exp(-2 T0/t) ] [1-exp(-2 T0/t) ] est supérieur à [1-exp(-T0/t)] , donc Q0 est inférieur à Q'. Tracer sur un même graphe QC(t) et QS(t) en fonction du temps. Pour un rythme cardiaque de 50 cycles ( systole + diastole) par minute, quelle est la valeur de T0 ? 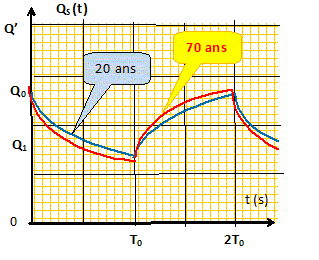Durée d'un cycle =2T0 = 50/60 =0,83 s ; T0 =0,416 ~ 0,42 s. Quelle est la dimension de la résistance hydrodynamique R du système capillaire ? pression ( Pa) divisée par un débit (m3 s-1) : Pa s m-3. On donne R= 18 mm Hg min L-1. Quelle est la valeur de R en unité S.I ? 1 mm Hg = 0,001*9,8*13600 = 133 Pa ; 1 min = 60 s ; 1 L = 10-3 m3. R = 18*133*60 / 10-3 = 1,44 108 Pa s m-3. Sachant que e-0,7 ~ 0,5, calculer Q0/Q' et Q1/Q' : - pour C= 6 cm3 kPa-1 ( individu de 20 ans) C = 6 10-6/1000 =6 10-9 m3 Pa-1 ; t = RC = 1,44 108 *6 10-9 =0,864 s ; T0 / t =0,42 /0,864 =0,486. exp(-T0/t) = exp(-0,486) = 0,615. Or Q0 exp(-T0/t) = Q1 d'où Q1 /Q0 =0,615~ 0,62. 1- exp(-2T0/t) =1- exp(-0,972) = 0,622 ; 1- exp(-T0/t) =1- 0,615 = 0,385 ; Q0/Q' =0,385/0,622= 0,62. Q1/Q' =0,62*0,62 = 0,38. - pour C= 2 cm3 kPa-1 ( individu de 70 ans) C = 2 10-6/1000 =2 10-9 m3 Pa-1 ; t = RC = 1,44 108 *2 10-9 =0,288 s ; T0 / t =0,288 / 0,42 =0,686. exp(-T0/t) = exp(-0,686) = 0,50. Or Q0 exp(-T0/t) = Q1 d'où Q1 /Q0 =0,50~ 0,5. 1- exp(-2T0/t) =1- exp(-1,37) = 0,746 ; 1- exp(-T0/t) =1- 0,50 = 0,50 ; Q0/Q' =0,5/0,746 = 0,67. Q1/Q' =0,5*0,67 = 0,34. Pour quel individu, le débit dans le système capillaire est-il le plus régulier ? individu de 20 ans : Q0-Q1 =0,24 Q'. ( 0,33 Q' pour la personne de 70 ans).

retour -menu