Champ magnétique crée par un fil ; densimètre, aldehyde et cétone ; chute et rebond

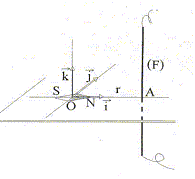
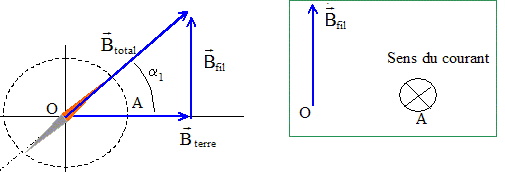
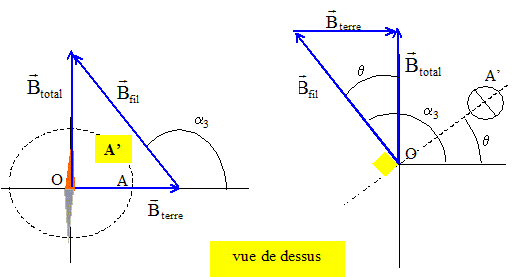
Un fil rectiligne infini, parcouru par un courant électrique I crée, en un point distant de r, un champ magnétique B = m0 I/(2pr) avec m0 = 4p 10-7 S.I. L'aiguille aimantée d'une boussole est orientée suivant l'axe (O i), la pointe nord N dans le sens de i. Un fil conducteur verticale très long F peut être déplacé autour de O sur une circonférence de rayon r = 10 cm. (F) est en A ( r,0, 0) lorsqu'on envoie un courant I0 = 10 A dans (F), l'aiguille aimantée tourne alors d'un angle a1 =(i , SN) =45° dans le plan horizontal. Préciser le sens du courant électrique dans (F). La boussole s'oriente suivant le champ magnétique total, somme vectorielle du champ magnétique terrestre et du champ crée par le fil. La règle de l'observateur donne le sens du courant, connaissant le sens du champ crée par le fil : le courant I descend le fil.   (F) étant toujours placé en A, on envoie dans le fil un courant de même sens mais d'intensité 2I0. Calculer l'angle a2. tana1 =tan 45 ° = 1 =B1 fil / Bterre d'où B1 fil = Bterre B1 fil = m0 I0/(2pr)   tan a2 =B 2 fil / Bterre = B 2 fil / B1 fil avec B2 fil = m0 2I0/(2pr) tan a2 =2 ; a2 = 63,4°. En quel point A', distant de OA'=r=10 cm du point O, doit-on placer (F) parcouru par le courant précédent I=2I0 pour que l'aiguille fasse un angle a3 = +90 °, c'est à dire s'orientant suivant j. On donnera la position de A' par l'angle q =(i, OA') et par ses coordonnées dans (O, i, j). sin q = Bterre / B 2 fil = B1 fil / B 2 fil = 0,5 ; q =30°. xA' = r cos 30 = 10 *0,866 = 8,67 cm. yA' = r sin 30 = 10 *0,5= 5 cm.   Un densimètre est constitué d'un flotteur de volume V0 surmonté d'une tige cylindrique de section s et de hauteur H. Le flotteur est lesté pour stabiliser l'appareil en position verticale. On plonge le densimètre, de mase M, dans un liquide de masse volumique m et on note h la hauteur immergée de la tige. 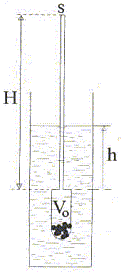Ecrire la condition d'équilibre du densimètre et établir la relation donnant m en fonction de M, V0, h et s. Le densimètre est en équilibre sous l'action de son poids ( valeur Mg) et de la poussée d'Archimède. Ces deux forces sont opposées et ont même valeur. Volume du densimètre immergé : V0+hs. Poussée d'Archimède = poids du volume de liquide déplacé : mg(V0+hs) d'où : Mg = mg(V0+hs) ; M = m(V0+hs) ; m = M/(V0+hs). Calculer V0 si dans l'eau h = 15,0 cm. M= 50,00 g ; s = 1,00 cm2 ; meau = 1000 kg m-3. V0+hs = M/m ; V0 = M/m- hs avec M = 0,05 kg ; s = 10-4 m2 ; h = 0,15 m. V0= 0,05/1000 -0,15 10-4 =3,50 10-5 m3 = 35,0 cm3.  On plonge le densimètre successivement dans deux liquides diférents ; les hauteurs immergées sont respectivement h1 = 19,3 cm et h2 = 6,7 cm. Calculer les densités d1 et d2 de ces liquides. g = 9,81 N/kg. m = M/(V0+hs) m1 =0,05 / (35 10-6 + 0,193 10-4) =921 kg m-3 = 0,921 g cm-3 ; d1 = 0,921. m2 =0,05 / (35 10-6 + 0,067 10-4) =1,20 103 kg m-3 = 1,20 g cm-3 ; d2 = 1,20. L'oxydation complète par le dioxygène de 0,87 g d'une substance organique A (CxHyOz) fournit 1,975 g de CO2 et 0,819 g de H2O. Ecrire l'équation bilan de la réaction. CxHyOz + (x +0,25 y-0,5z)O2 = x CO2 + 0,5y H2O. Déterminer la composition centésimale en masse (%C, %H, %O). Dans 1,975 g de CO2 il y a : 1,975*12/44 = 0,5386 g de carbone. Soit 0,5386/0,87 *100 = 61,9 % de carbone dans A. Dans 0,819 g d'eau il y a : 0,819*2/18 = 0,091 grame d'élément hydrogène. Soit 0,091/0,87*100 = 10,5 % H dans A. Puis 100-61,9-10,5 = 27,6 % élément oxygène dans A. Trouver une relation entre x et y et entre y et z. 12 x / 61,9 = y / 10,5 soit x = 0,491 y ; x~0,5 y. y / 10,5 = 16 z/27,6 soit z= 0,164 y ou y~6z. Déterminer la formule brute sous la forme (CmHnOb)y. m, n, b et y sont des entiers. CxHyOz s'écrit : C0,5yHyO0,164 y ou encore (C3H6O)y. Que devient la formule brute si y=1 ? C3H6O. A quelles familles de composés oxygénés correspond cette formule ? Aldehyde ou cétone en se limitant aux composés non cycliques. Donner les formules semi-développées possibles et leurs noms. CH3-CH2-CHO propanal ; CH3-CO-CH3 : propanone ou acétone. Une balle de masse m = 100g est lâchée sans vitesse d'une hauteur h = 1 m. g = 10 N/kg La balle rebondit sur le sol. L'énergie cinétique juste après le rebond est égale à l'énergie cinétique juste avant multipliée par une constante k = 0,9. Quelle est la vitesse de la balle juste après un rebond ? L'énergie mécanique initiale est sous forme potentielle de pesanteur ( origine au sol) : mgh0. L'énergie mécanique juste avant de toucher le sol est sous forme cinétique : ½mv02. Par suite de la conservation de l'énergie mécanique : ½mv02 = mgh0. Juste après le premier rebond l'énergie cinétique vaut : 0,9*(½mv02) = 0,9 mgh0 = ½mv12. d'où : v12 = 1,8 gh0 ; v1=( 1,8 gh0 )½ =( 1,8 *10*1 )½=4,24 m/s. Quelle est l'altitude maximale atteinte après un rebond ? Conservation de l'énergie mécanique lors de la remontée après le premier rebond : 0,9 mgh0 = mgh soit h = 0,9 h0 = 0,9*1 = 0,9 m. Quelle est la durée de la seconde descente ? h = ½ gt2 soit t = (2h/g)½=(1,8/10)½=0,42 s.

retour -menu