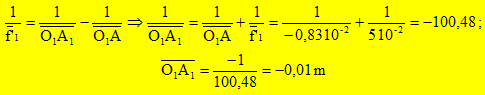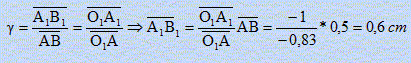optique : diamètre apparent, loupe, oculaire du microscope lycée.

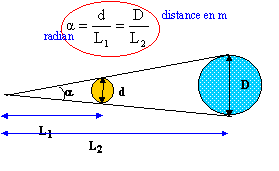
Dans tout l'exercice l'objet noté AB sera considéré comme un objet plan perpendiculaire à l'axe optique des instruments utilisés, le point A étant sur l'axe et la taille de AB étant de 0,5 cm. Diamètre apparent : Définir le diamètre apparent d'un objet vu à partir d'un point O. Faire un schéma explicatif. Cette notion est utilisée dans les cas suivants : - objet de petite dimension ( moins de quelques centaines de microns) observé à quelques dizaines de cm - objet de grande dimension ( astre ) éloigné de l'observateur. On peut alors confondre l'angle en radian et sa tangente : Le diamètre apparent est un angle : rapport du diamètre de l'objet à la distance objet-observateur. Calculer le diamètre apparent a de AB vu d'un point O situé à 25 cm de l'objet et dans une direction perpendiculaire à l'objet. a = AB 25 = 0,5 25 = 2 10-2radian. 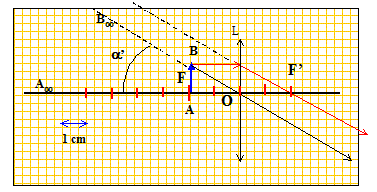La loupe : On dispose d'un loupe assimilable à une lentille mince convergente de vergence 40 dioptries. Où doit on placer l'objet AB pour que son image soit à l'infini ? L'objet doit être au foyer objet de la lentille convergente, c'est à dire à 1/40 = 0,025 m = 2,5 cm à gauche de la lentille. Sur votre copie tracer un schéma à l'échelle deux avec la lentille, l'axe optique, le centre optique, les foyers objet et image F et F', l'objet AB pour que l'image soit à l'infini, deux rayons particuliers issus de B et enfin l'image A'B'. Pour observer l'image où doit on placer l'oeil ? L'oeil doit être à droite de la lentille et regarder à travers la lentille. Calculer le diamètre apparent a ' de cette image vue depuis le foyer de la lentille. tana' ~a' AB OF = 0,5 2,5 = 2 10-1 radian. En déduire que le grossissement de cette loupe, défini par G = a' / a , est égal à 10. G = 0,2 / 0,02 = 10.  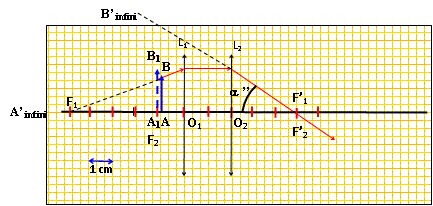L'oculaire d'un microscope : Un oculaire joue le même rôle qu'une loupe. Cependant les loupes trop grossissantes présentent divers défauts, appelés aberrations, qui nuisent à la qualité des images (phénomène d'irrisation (apparition des couleurs de l'arc en ciel) et de déformation de l'image (gonflement, rétrécissement)). Pour y remédier un oculaire de microscope n'est donc pas constitué d'une seule lentille mais d'un ensemble de deux lentilles minces convergentes de même axe optique, distantes de 2 cm. (L1) ,située du côté de l'objet, a une distance focale de 5 cm, celle de (L2) étant 3 cm. On observe avec cet oculaire le même objet AB situé à 0,83 cm de O1. On appelle A1B1 l'image de AB à travers (L1) , et A'B' l'image définitive. Montrer par le calcul que A1 est confondu avec F2.   En déduire la position de A'B'. L'image intermédiaire A1B1 joue le rôle d'objet pour la lentille (L2) : l'image A'B' d'un objet situé au foyer d'une lentille convergente est à l'infini. Calculer la taille de A1B1. Le grandissement transversal s'écrit : Sur la figure tracer la marche du rayon lumineux issu de B et se déplaçant parallèlement à l'axe optique entre les deux lentilles. On appelle a'' l'angle entre le rayon précédent sortant de (L2) et l'axe optique. Cet angle étant le diamètre apparent de l'image A'B' montrer que a'' = A1B1 / O2F'2. tana' ~a' A1B1 O2F'2 = 0,6 3 = 2 10-1 radian. En déduire que le grossissement de cet oculaire est le même que celui de la loupe précédente. G = a' / a ; G = 0,2 / 0,02 = 10.

retour -menu