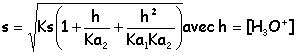|
Solubilité : effet d'ion commun ; influence du pH. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le sulfate de plomb a un produit de solubilité égal à Ks=1,6.10-8. MPb = 207,2 g.mol-1 MS = 32 g.mol-1 MO = 16 g.mol-1 Calculer la solubilité s dans l'eau et la masse de sulfate de plomb soluble dans 200 cm3 d'eau. PbSO4(s) = Pb2+ + SO42-. Ks=[Pb2+][SO42-] La solution est électriquement neutre : s = [Pb2+]=[SO42-] Ks= s2 doù s = (1,6.10-8)½ =1,3 10-4 mol/L. Calculer la solubilité s1 dans une solution décimolaire de nitrate de plomb. [Pb2+] = (0,1+s1); [SO42-] =s1 ; Ks =s1 (0,1+s1) s12 + 0,1 s1 -1,6.10-8 =0 ; hypothèse : s12 terme négligeable : résoudre s1 ~1,6.10-7 mol/L. s12 = 2,6 10-14 ( l'hypothèse est bien vérifiée ) Calculer la solubilité s2 dans une solution à 0,001 mol.L-1 de sulfate de sodium. [SO42-] = (0,001+s2) ; [Pb2+] =s2 ; Ks =s2 (0,001+s2) s22 + 0,001 s2 -1,6.10-8 =0 ; résoudre s2 ~1,58.10-5 mol/L.
Solubilité du chromate d'argent : Sachant qu'à 25 °C le produit de solubilité du chromate d'argent est Ks = 3.10-12. Calculer la solubilité du chromate d'argent Ag2CrO4. Ag2CrO4 solide = 2Ag+ + CrO42-. Ks = [Ag+]2[CrO42-] ; on pose s= [CrO42-] ; solution électriquement neutre : [Ag+] = 2 [CrO42-] d'où [Ag+] = 2 s Ks = (2s)² s = 4 s3 = 3 10-12 soit s3 = 0,75 10-12 prendre la racine cubique : s = 9,1 10-5 mol/L. Que devient cette solubilité dans une solution aqueuse de chromate de potassium K2CrO4 à 0,01 mol.L-1 ? [CrO42-] = (0,01+s1); [Ag+] =2s1 ; Ks = 4s12 (0,01+s1) 4s13 + 0,04 s12 -3 10-12 =0 ; hypothèse : s13 terme négligeable : résoudre s1 ~8,7.10-6 mol/L. s13 = 6,5 10-16 ( l'hypothèse est bien vérifiée ). Que devient la solubilité si à 100 cm3 de solution saturée de chromate d'argent, on ajoute sans variation de volume, 0,01 mole de nitrate d'argent ? 0,01 mole d'ion argent dans 100 mL soit 0,1 mol d'ion argent ajoutée dans 1 L. hypothèse :
s2 terme négligeable devant 0,1 :
3
10-12
=0,01 s2 résoudre
s2
~3.10-10
mol/L. (
l'hypothèse est bien vérifiée
). On donne pour l'acide carbonique: pKa1 = 6,4 pKa2 = 10,3. Le produit de solubilité du carbonate de calcium vaut Ks = 8,7.10-9. Exprimer la solubilité s du carbonate de calcium en fonction de h (concentration en ions oxonium). CaCO3(s) = Ca2+ + CO32- ; Ks =[Ca2+][CO32-]total s=[Ca2+]=[CO32-] + [HCO3-] + [CO2,H2O] ; Ks =s ( [CO32-] + [HCO3-] + [CO2,H2O])
Comment évolue la solubilité avec le pH ? Justifier. Si le pH augmente, h diminue et en conséquence : Ks, Ka1 et Ka2 étant constants à température constante)
Calculer la solubilité à pH = 5 et pH = 10. à pH=5 :
s = [ 8,7.10-9(1 + 2 105 + 8 106)]½ =0,27 mol/L. à pH=10 :
s = [ 8,7.10-9(1 + 2]½ =1,6 10-4 mol/L.
Solubilité du sulfure d'argent : Quelle est la solubilité molaire de Ag2S, le film noir qui se forme sur les objets en argent ? pKS (Ag2S) = 50,2 ; M (Ag) = 108 g.mol-1 M (S) = 32 g.mol-1. Ag2S (s) = 2 Ag+ + S2-. Ks = [Ag+]2[S2-] on pose s= [S2-] ; solution électriquement neutre : [Ag+] = 2[S2-] d'où [Ag+] = 2 s Ks = (2s)² s = 4 s3 = 10-50,2 soit s3 = 1,58 10-51 prendre la racine cubique : s = 1,16 10-17 mol/L. Quelle est sa solubilité molaire dans AgNO3 à 2.10-4 mol.L-1 ? [Ag+] = (2 10-4+2s1); [S2-] =s1 ; Ks = (2 10-4+2s1) 2 s1. hypothèse : s1 terme négligeable devant 2 10-4 : 4 10-8 s1 = 10-50,2 résoudre s1 ~1,58.10-43 mol/L. ( l'hypothèse est bien vérifiée ). Quelle masse de Ag2S peut-on dissoudre dans 10 litres de la solution précédente ? 1,58 10-43*10 = 1,58 10-42 mol d'ion sulfure dans 10 L soit 1,58 10-42 mol de soluté Ag2S. Masse molaire Ag2S : M = 2*108+32 =248 g/mol puis m = 248*1,58 10-42 =3,9 10-40 g.
L'éthanoate d'argent (CH3COOAg) est peu soluble dans l'eau. On donne KS = 2.10-3. L'acide éthanoïque est un acide faible : pKa = 4,8. Calculer la solubilité s sans tenir compte de l'action des ions sur l'eau. CH3COOAg (s) = Ag+ + CH3COO-. Ks = [Ag+][ CH3COO-]. La solution est électriquement neutre : s = [Ag+]=[ CH3COO-] ; Ks = s2 = 2 10-3 ; s = 4,47 10-2 mol/L. Quel est le pH de la solution saturée ? Le couple acide / base CH3COOH / CH3COO- fixe le pH : pH= pKa = log [CH3COO-] / [CH3COOH ] Le tableau ci-dessous est établi pour un volume V= 1 L.
Le produit ionique de l'eau, à 25 °C, conduit à : [H3O+]= 10-14 / 5,3 10-6 = 1,9 10-9. pH = 8,7. L'approximation faite pour le calcul de s est-elle justifiée ? Taux d'avancement final : xf /xmax =5,3 10-6/ 4,47 10-2 ~ 10-4. L'ion éthanoate réagissant très peu avec l'eau, l'approximation est justifiée. En réalité la solubilité est-elle supérieure ou inférieure à la valeur calculée ? Justifier la réponse. CH3COO- + H2O = CH3COOH + HO-(1) CH3COOAg (s) = Ag+ + CH3COO-(2) Une faible partie des ions éthanoate disparaît suivant (1) : en conséquence l'équilibre (2) est déplacé dans le sens direct : la solubilité est un peu plus grande que celle calculée.
A 100 cm3 d'une solution d'éthanoate de sodium à 0,2 mol.L-1, on ajoute 100 cm3 d'une solution de nitrate d'argent à 0,2 mol.L-1. On donne MAg = 108 g.mol-1. Montrer qu'il y a précipitation et calculer la masse du précipité obtenu. Volume total de la solution : V = 0,2 L ; [Ag+]i =0,2*0,1/0,2 = 0,1 mol/L. [CH3COO- ]i =0,2*0,1/0,2 = 0,1 mol/L. CH3COOAg (s) = Ag+ + CH3COO- : Ks = 2 10-3 ; quotient initial de réaction Q r i =[Ag+]i [CH3COO- ]i = 0,02 Q r i > Ks : l'équilibre est déplacé vers la gauche, sens indirect, précipitation de l'éthnoate d'argent. Or s =[Ag+]fin= 4,47 10-2 mol/L; quantité de matière d'ion argent ayant précipité : (0,1-4,47 10-2)*0,2 =1,1 10-2 mol. Quantité de matière de précipité : n=1,1 10-2 mol. M(CH3COOAg) =2*12+3+32+108=167 g/mol. mase de précipité : m = n M = 0,011*167 =1,8 g. On tient compte de l'influence du pH sur la solubilité. Établir la relation entre s, [H3O+], Ks et Ka. s=[Ag+]=[CH3COO- ] + [CH3COOH ] ; Ks =s ( [CH3COO- ] + [CH3COOH ] ) Or la constante d'acidité de l'acide éthanoïque donne :
Calculer la valeur de s pour pH = 7 et pour pH = 4,5. pH= 7 : s2 =2 10-3(1+10-7/10-4,8) ; s =4,48 10-2 mol/L. pH= 4,5 : s2 =2 10-3(1+10-4,5/10-4,8) ; s =7,74 10-2 mol/L. Justifier qualitativement l'évolution de s lorsque le pH diminue. CH3COO- + H3O+ = CH3COOH + H2O (1) CH3COOAg (s) = Ag+ + CH3COO-(2) Une petite partie des ions éthanoate disparaît suivant (1) quand le pH augmente : en conséquence l'équilibre (2) est déplacé dans le sens direct : la solubilité augmente. Solubilité du carbonate de baryum : On veut dissoudre du carbonate de baryum dans une solution de pH variable. On donne pour l'acide carbonique: pKa1 = 6,4 ; pKa2 = 10,3. pKs (BaCO3) = 8,3 ; M (BaCO3) = 197 g.mol-1. Exprimer la solubilité s du carbonate de baryum en fonction de h, Ka1 , Ka2 et Ks. Voir exercice ci-desus
: Donner l'expression de log s = f(pH) pour 7,5 < pH < 9 . à pH = 7,5 : h/Ka2 ~630 ; h2/(Ka2Ka1) ~50 ; s ~ (Ksh/Ka2 )½ ; à pH =9 : h/Ka2 ~20 ; h2/(Ka2Ka1) ~0,05 ; s ~ (Ksh/Ka2 )½ ; log s = ½(log Ks -log Ka2 + log h) ; log s = ½( pKa2 - pKs -pH) = 1-0,5 pH. Déterminer la valeur du pH nécessaire pour pouvoir dissoudre 50 mg de carbonate de baryum dans 500 mL d'eau. 0,1 g dans 1 L ; s =0,1 / 197 = 5,1 10-4 mol/L ; log s = -3,3 ; pH =2(1-log s) ; pH= 8,6.
Solubilité du chlorure d'argent dans différentes solutions :
Le produit de solubilité du chlorure d'argent est Ks= 1,8 10-10 à 25 °C. Calculer sa solubilité : a/ dans l'eau pure. AgCl(s) = Ag+ + Cl- ; Ks= [Ag+][Cl-]=s2 =1,8 10-10 ; s = 1,34 10-5 mol/L. b/ dans une solution de nitrate d'argent à 0,2 mol.L-1. [Cl-]=s1 ; [Ag+]= (0,2+s1) ; Ks=(0,2+s1)s1. Hypothèse s1<<0,2 : 1,8 10-10 = 0,2 s1 ; s1 =1,8 10-10 /0,2 = 9,0 10-10 mol/L. ( l'hypothèse est bien vérifiée). c/ dans une solution d'acide chlorhydrique à 0,5 mol.L-1. [Ag+]=s2 ; [Cl-]= (0,5+s2) ; Ks=(0,5+s2)s2. Hypothèse s2<<0,5 : 1,8 10-10 = 0,5 s2 ; s2 =1,8 10-10 /0,5 = 3,6 10-10 mol/L. ( l'hypothèse est bien vérifiée).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|