amplificateur opérationel, Millman, équation différentielle et nombres complexes concours ITPE 2008

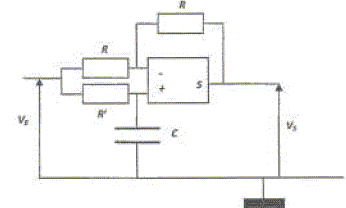
On considère le circuit ci-dessous comprenant un amplificateur opérationnel supposé parfait et fonctionnant en régime linéaire. Rappeler les proprités d'un amplificateur opérationnel parfait. qon précisera les résistances d'entrée et de sortie dans ce cas. L'impédance d'entrée est infinie, celle de sortie est nulle. Les intensités des courants d'entrée sont nulles. Les potentiels des deux entrées sont identiques  Quels sont les ordres de grandeurs des résistances d'entrée et de sortie d'un amplifiateur opérationnel réel ? Impédance d'entrée supérieure à  10 MW ; impédance de sortie inférieure à 200 W.   Déterminer la fonction de transfert H = Vs / Ve en régime sinusoïdal. 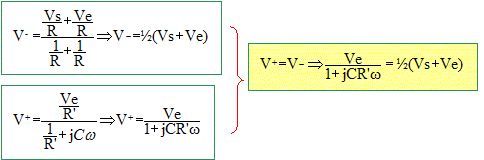Exprimer les potentiels des deux entrées E+ et E- à partir du théorème de Millman :     2Ve = (Vs+Ve)(1+jCR'w) Ve (1- jCR'w)= Vs (1+jCR'w) Vs /Ve = (1- jCR'w) / (1+jCR'w) = (1- jCR'w)2 / [1 + (CR'w)2] H =(1- jCR'w)2 / [1 + (CR'w)2].     Déterminer le module de H et en déduire la fonction de ce montage.  H =(1- jCR'w)2 / [1 + (CR'w)2] =(1-( CR'w)2 -2jCR'w) / [1 + (CR'w)2] | H | = [[(1-( CR'w)2 ]2 +( 2CR'w)2]½ / [1 + (CR'w)2] | H | =[(1+( CR'w)4 -2(CR'w)2 +4(CR'w)2]½ / [1 + (CR'w)2] | H | =[(1+( CR'w)4 +2(CR'w)2 ]½ / [1 + (CR'w)2] | H | =[[(1+( CR'w)2 ]2 ]½ / [1 + (CR'w)2] ; | H | = 1. La tension de sortie est identique à la tension d'entrée. On supose maintenant que VE=0 pour t<0 et VE=E0 pour t>0.  Etablir l'équation différentielle vérifiée par Vs. 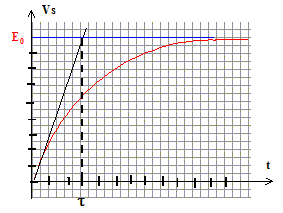Ve (1- CR'jw) = Vs (1+CR'jw)   Or la multiplication par jw correspond à la dérivation d / dt : Ve +CR' dVe/dt = Vs + R'C dVs/dt Or Ve = E0 d'où dVe/dt = 0 et par suite : Ve = Vs +R'C dVs/dt dVs/dt +1/(R'C) Vs = E0/(R'C) (1)  En déduire l'expression de Vs. Tracer Vs(t).  On pose : t =R'C . Solution particulière de (1) ( régime permanent) : Vs = E0. solution générale de l'équation sans second membre : Vs= A exp(-t/t).  Solution générale de (1) : Vs = A exp(-t/t)+E0. condition initiale : Vs=0 d'où A = -E0. Vs = E0(1- exp(-t/t) ).

retour -menu