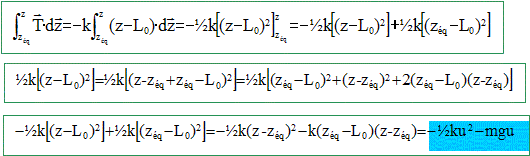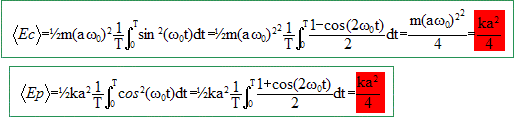oscillateur élastique vertical concours ITPE 2008

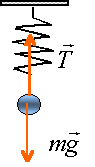
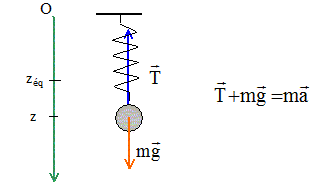
Une sphère, supposée ponctuelle, de masse m=100 g est suspendue à un ressort vertical sans masse, de raideur k dans un champ de pesanteur uniforme d'intensité g. L'autre extrémité du ressort est fixe en O. Le problème est paramétré par un axe vertical orienté vers le bas. On notera z l'abscisse de la sphère. Déterminer la position d'équilibre zéq de la sphère en fonction de la longueur à vide du ressort L0, m, g et k.   A l'équilibre le poids est opposé à la tension et la tension est proportionnelle à l'allongement du ressort. mg=k(Léq-L0) ; masse en kg ; Léq-L0 en mètre ; zéq = Léq. zéq = L0 + mg/k.  On écarte la sphère de sa position d'équilibre et on lache la sphère sans vitesse initiale. Etablir l'équation du mouvement de la sphère. Ecrire la seconde loi de Newton sur l'axe Oz : -k(z-L0)+mg=mz" -k(z-zéq +zéq -L0)+mg = mz" ; -k(z-zéq ) -k(zéq -L0)+mg = mz" Or k(zéq -L0)= mg d'où : -k(z-zéq ) = mz". On choisit la position d'équilibre comme nouvelle origine en posant u = z-zéq : il vient : -ku = mu" soit u" +k/m u= 0 ; u"+w02u = 0 (1) avec w02 = k/m. Quel est la nature du mouvement ? (1) est l'équation différentielle d'un oscillateur harmonique : mouvement sinusoïdal périodique non amorti. Donner la position u de la sphère par rapport à la position d'équilibre en fonction du temps ; on note u(t=0) = a. u(t) = A cos ( w0t+j) à t=0, u(0) = a = A cosj ; d'où j =0 et A=a. u(t) = a cos ( w0t). Proposer deux méthodes expérimentales permettant de déterminer k. méthode statique : Accrocher une masse m au ressort et mesurer son allongement x : à l'équilibre, le poids a même valeur que la tension. mg = kx d'où k = mg/x mesure de la période des petites oscillations : Faire osciller le système {ressort + masse acrochée à l'extrémité} dans un plan vertical en écartant le ressort de 10 degrés par rapport à la verticale. Mesurer la durée de 10 oscillations ( 10 périodes T) T = 2p(m/k)½ ; k = 4p2m/T2. Etablir l'expression de l'énergie potentielle de pesanteur.  On choisit l'origine de l'énergie potentielle à la position d'équilibre zéq. Travail du poids mg pour passer de la position zéq à la position z >0 : mg(z-zéq) La variation de l'énergie potentielle de pesanteur est l'opposé du travail du poids : DEpp = mg(zéq-z) En posant u = z-zéq : DEpp = -mgu DEpp =Epp(z) - Epp(zéq) = -mgu-0 d'où Epp(u) = -mgu.   Etablir l'expression de l'énergie potentielle élastique du ressort. On choisit l'origine de l'énergie potentielle à la position d'équilibre zéq. 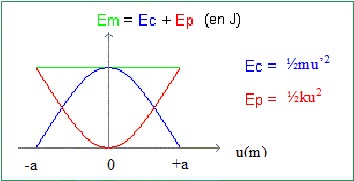Travail de la tension T= -k(z-L0) pour passer de la position zéq à la position z >0 : La variation de l'énergie potentielle élastique est l'opposé du travail de la tension : DEpé = ½ku2+mgu DEpé =Epé(z) - Epp(zéq) = ½ku2+ mgu d'où Epé(u) = ½ku2+ mgu. Total énergie potentielle : Ep = ½ku2.  Dans quelle condition peut-on considérer le système comme conservatif ? Si seule la tension et le poids travaillent ( absence de frottements) le système est conservatif. Tracer sur un même graphique les courbes représentant l'énergie mécanique et l'énergie potentielle du système en fonction de u.      Montrer comment on peut lire la valeur de l'énergie cinétique.   Energie cinétique = énergie mécanique - énergie potentielle Energie mécanique = ½ka2. Montrer qu'en moyenne il y a équipartition de l'énergie cinétique et de l'énergie potentielle.

retour -menu