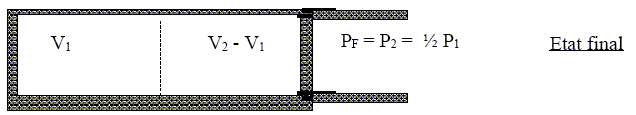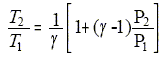|
Etude d'un cycle moteur, étude de transformations adiabatiques. concours interne ITPE 07
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Gaz parfait Rappeler la ou les définitions d’un gaz parfait. Modèle thermodynamique : dans un gaz à basse pression les interactions électrostatiques entre particules sont négligeables, les molécules étant suffisamment éloignés les unes des autres. Dans un gaz réel, il faut prendre en compte les interactions entre particules et tenir compte du volume des molécules constituant le gaz. Donner un exemple de système assimilable à un gaz parfait puis à un gaz réel. Un gaz quelconque, sous faible pression, peut être assimilé à un gaz parfait. Un gaz, dans des conditions proches de la liquéfaction, ne peut pas être assimilé à un gaz parfait.
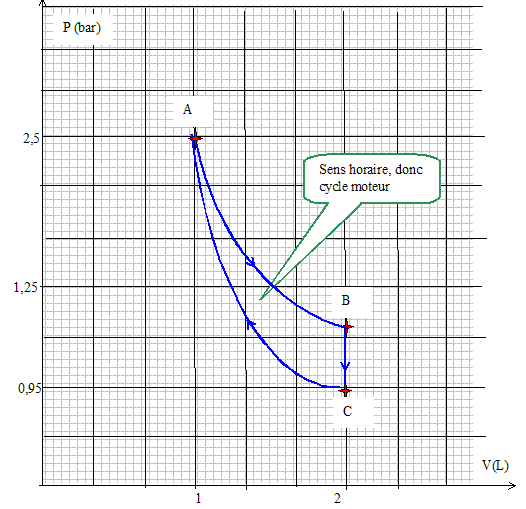
Etude d'un cycle moteur. On étudie n moles de gaz parfait auxquelles on fait décrire le cycle ABC suivant : AB est une isotherme à la température T1 = TA = TB . BC est une isochore qui fait passer le système de TB à TC = T2 . CA est une adiabatique. Les trois transformations sont réversibles. Données : R = 8,32 J.K-1.mol-1 ; g =CP/CV=1,4. Compléter le tableau suivant :
Loi des gaz parfaits : PB= nRTB/VB=0,08*8,32*375/(2 10-3 )=1,25 105 Pa = 1,25 bar. Loi de Laplace : PAVAg =PCVCg ; PC= PA(VA/VC)g =2,5(1/2)1,4 =0,95 bar. TC = PCVC/(nR)=0,95 105*2 10-3 /(0,08*8,32) =285 K. Dessiner le cycle dans un diagramme (P,V). Justifier que le cycle est moteur.
thermique) échangés avec l’extérieur. A--> B isotherme : la variation d'énergie interne est nulle : WAB+QAB=0 (1). dW=-PdV = -nRTA dV/V = -nRTA d ln(V) WAB=-nRTA
ln(VB/VA)
=-0,08 *8,32*375 ln 2 = -173
J.
(1)
donne : QAB=173
J.
DUBC= n CVDT = WBC+QBC=QBC. QBC=n
CV(TC-TB)
=nR/(g-1)(TC-TB)
= 0,08*8,32/0,4*(285-375) ; QBC=
-150
J.
DUCA= n CVDT = WCA+QCA=WCA. WCA=n CV(TA-TC) =nR/(g-1)(TA-TC) = 0,08*8,32/0,4*(375-285) ; WCA= = +150 J.
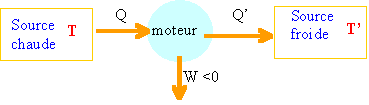
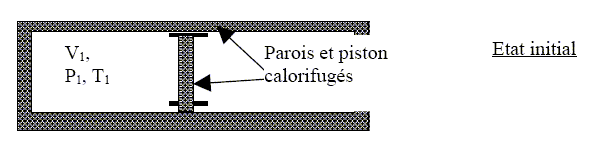
Le rendement est égal au travail utile divisé par l'énergie prélevée à la source chaude. rm = -W /QAB= 23/173 = 0,13. Comparer la valeur obtenue pour le rendement de ce cycle avec celle d’un cycle de Carnot dont le rendement rc vaudrait dans les mêmes conditions de température : rC= 1-TC/TA= 1-285/375 = 0,24. Comparer les performances des deux cycles et conclure. Le rendement est maximum lorsque toutes les transformations sont réversibles ( cas du cycle de Carnot). Etude de transformations adiabatiques. On étudie les transformations adiabatiques des n moles précédentes du même gaz parfait. Le gaz est contenu dans un récipient calorifugé et on lui fait subir trois détentes adiabatiques : la première transformation est quasi-statique, la deuxième est monobare, et la troisième se fait dans le vide. On cherche à comparer le travail fourni au milieu extérieur par la détente ainsi que l’entropie créée selon les modalités de la transformation. L’état initial est défini par P1, V1, et T1 donnés. Les trois transformations conduisent à la même pression finale PF = P2 = ½ P1. On note V2 et T2 le volume et la température de l’état final qui peuvent être différents après chaque transformation. Données numériques : P1 = 2 bar ; V1 = 1 L ; T1 = 300 K ; g=1,4.
Généralités. Rappeler le second principe de la thermodynamique. L'entropie d'un système isolé ne peut qu'augmenter jusqu'à une valeur maximale correspondant à un état d'équilire Etablir l’expression DS de la variation de la fonction entropie S de n moles d’un gaz parfait. Expression de l'entropie d'un gaz parfait de coefficient g constant en fonction du volume V et de la température T: dS= dU/T+P/T dV avec P/T = nR/V et dU=nCvdT = nR/(g-1) dT d'où dS= nR/(g-1) d (lnT) + nR d(ln V) par intégration : S-S0= nR[1/(g-1) ln(T/T0) + ln(V/V0)]. Pour une transformation adiabatique d’un gaz parfait, exprimer l’entropie échangée par le système avec l’extérieur, Se, et l’entropie créée, Sc, au cours de la transformation. Se = Q/T ; Sc = DS-Se.
La première transformation se fait de façon quasi-statique. Définir ce terme. Proposer un mode opératoire. Echange réalisé en un grand nombre d'étapes afin que le déséquilibre entre les grandeurs intensives se réalise par des variations très faibles. Déplacer très lentement le piston.
Déterminer et calculer V2 et T2 lorsque la pression du gaz à l’état final, P2, est diminuée de moitié par rapport à l’état initial (P2 = ½ P1). l'opérateur relâche très lentement le piston : transformation réversible P1V1g=P2V2g soit V2 = V1(P1/P2)1/g =1.(2)1/1,4 =1,64 L. T2 =P2V2 /(nR) =105 *1,64 10-3 /(0,08*8,32) = 246 K. Déterminer et calculer la variation d’énergie interne DU et le travail échangé W au cours de la transformation. Conservation de l'énergie ( premier principe ) DU= W+Q et DU= nCv(T2-T1). adiabatique réversible : Q=0 ; donc W = DU= nCv(T2-T1) =nR/(g-1)(T2-T1). W= 0,08*8,32/0,4*(246-300) ; W= -90 J. Déterminer et calculer DS, ainsi que Sc. L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. S-S0= nR[1/(g-1) ln(T2/T1) + ln(V2/V1)]. DS= 0,08*8,32[1/0,4 ln (246/300) + ln(1,64)]; DS =0 ( adiabatique) Bilan entropique : entropie échangée Se = Q/T = 0 ( enceinte calorifugée) entropie créee Sc = DS - Se = 0 J K-1, transformation réversible.
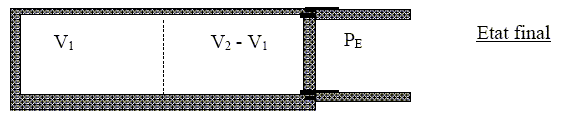
La deuxième détente se fait en débloquant une paroi afin d’équilibrer le système avec la pression extérieure constante PE = ½ P1= P2. Le tout restant calorifugé.
Définir le terme « monobare ». La transformation est adiabatique( cylindre calorifugé). Le piston se déplace rapidement quand on enlève la cale, la transformation n'est pas réversible. La pression finale est égale à la pression du milieu extérieur. Exprimer le travail W reçu par le gaz et la variation d’énergie interne DU pour la détente. W= -P2 ( V2-V1)= -P2 V2(1-V1/V2) Or P2V2/T2 = P1V1/T1= nR d'où : V1/V2= P2T1/ (P1T2 ) W = -P2 V2(1- P2T1/ (P1T2 )) ; W =-nRT2(1- P2T1/ (P1T2 )). La transformation est adiabatique : Q=0. variation d'énergie interne du gaz : DU= nCV (T2-T1) ; DU =nR/(g-1)(T2-T1). Montrer que les modalités
de la transformation imposent : D U= Q+W ( premier principe) : -nRT2 (1- P2T1/ (P1T2 ))= nR/(g-1)(T2-T1). -T2 [1- P2T1/ (P1T2 )]= 1/(g-1)(T2-T1) ; (T1-T2)/T2 =(g-1)[1- P2T1/ (P1T2 )] T1/T2-1 = (g-1)-(g-1)P2T1/ (P1T2 ) ; T1/T2 [1+(g-1)P2/ (P1] = g. d'où
: Calculer numériquement V2 , T2 , et le travail W. T2/T1 =1/1,4 [1+0,4*0,5]=0,857 ; T2 = 0,857 T1 =0,857*300 = 257,17 K ; T2 = 257 K. V2 = nRT2/P2 = 0,08*8,32*257,17/105 =1,71 10-3 m3; V2 = 1,7 L. W= -P2 ( V2-V1)= - 105(1,71-1) 10-3 ; W= -71 J.
Déterminer et calculer DS et Sc . L'entropie est une fonction d'état : en conséquence le chemin emprunté entre l'état initial et final importe peu ; le calcul de la variation d'entropie est fait pour une transformation réversibble. pour une transformation élémentaire : dS= dQ/T = (dU-dW)/T =n Cv /T dT+ PdV/T PV=nRT soit en différenciant :PdV+ VdP= nRdT ou PdV= nRdT-VdP dS= nCv /T dT +R/TdT-V/T dP= n(Cv +R)/T dT - RdP / P = nCP/T dT - Rd ln(P) = nCPmd ln(T) - Rd ln(P) DS=nCP ln(T2/T1) - R ln(P2/P1). avec CP = Rg/(g-1) DS=0,08*8,32*1,4/0,4 ln(257/300) - 8,32 ln0,5 =-0,36+ 5,77 ; DS= 5,4 J K-1. Justifier qualitativement que l’on peut « réduire » l’entropie créée en « fractionnant » la transformation étudiée en N étapes intermédiaires pour lesquelles la pression du gaz passe de Pk à Pk+1 = Pk + dP , avec dP << Pk . 3-9 En effectuant un développement limité adéquat à partir de l’expression de Sc établie à la question 3-5, montrer que pour une transformation élémentaire, effectuée entre les états intermédiaires définis par Pk et Pk+1 , l’entropie créée Sc,k tend vers 0. Confirmer ainsi la justification qualitative donnée en 3-8. Rappel : Pour e << 1 : ln(1+ e) ~ e ; (1+ e)a ~ 1+ae
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|