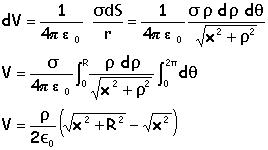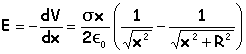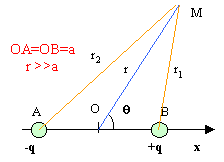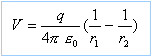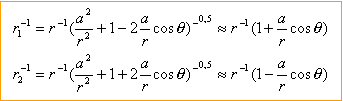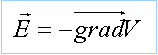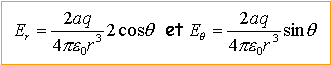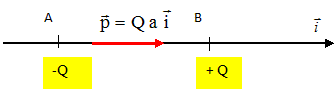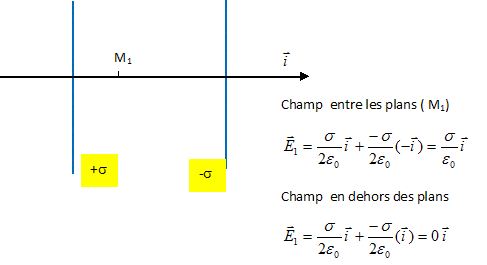Champ et potentiel électrostatiques Concours ITPE 2006.

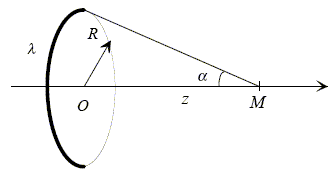
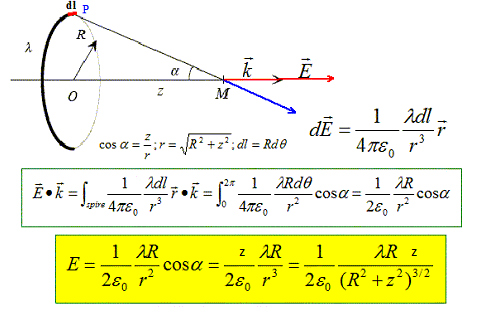
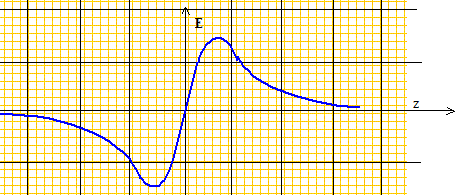
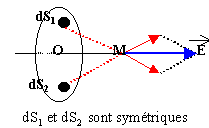
Les vecteurs sont écrits en gras et en bleu. On considère une spire circulaire de centre 0, de rayon R et d'axe dirigé par uz= k portant la densité linéique de charge l>0. Montrer qu'en tout point de l'axe, défini par OM =z ( z >0) , le champ E s'écrit : E(M) = lR 2e0 z (z2+R2)3/2 ux k est un vecteur unitaire porte par l'axe Oz.  Tout plan défini par le point M et un diamètre de la spire ne modifie par la distribution de la charge : E appartient à l'intersection de tous ces plans, c'est à dire que E est porté par l'axe Oz. Dans une symétrie par raport au plan contenant la spire, z devient -z : donc E(-z) = -E(z). Représenter sur un dessin les vecteurs E(x) et E(-x). Ces deux vecteurs sont de sens contraire. 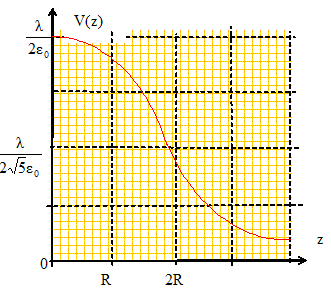Etablir l'expression du potentiel V(M) pour x>0. Rechercher une primitive de E ( E= - grad V) : on pose u = R2+z2 : du = 2z dz. z dz ( R2+z2)3/2 = 0,5 du u3/2 ; primitive : - u-0,5 = -1 ( R2+z2)1/2 Intégrer entre x=0 et l'infini ; la constante d'intégration est telle que le potentiel soit nul à l'infini. V(M) = lR 2e0 1 (z2+R2)1/2  Tracer E(z) et V(z) quel que soit x réel. E(z) et V(z) sont-elles des fonctions continues en O ? Justifier. 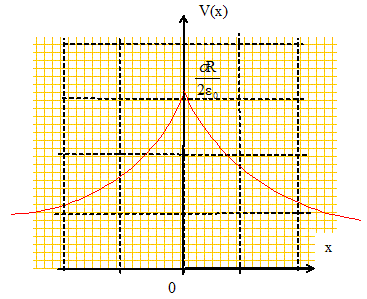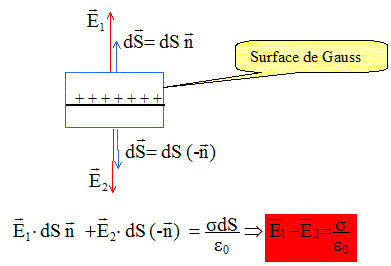V(z) est toujours une fonction continue ; E(z) est également continue : pas de traversée de surface chargée. Disque portant une charge surfacique . O : centre du disque ; R : rayon du disque ; s>0 : charge surfacique..  Montrer qu'en tout point de l'axe, défini par OM =x ( x >0) , le champ E s'écrit : E(M) = s 2e0 (1- x (x2+R2)1/2 ) ux Etablir l'expression du potentiel V(M) pour x>0.  L'élément de surface dS du disque porte la charge dq = s dS et crée en M (OM=x) le potentiel dV champ le champ résultant est dirigé vers le disque si la charge est négative. Tracer E(x) et V(x) quel que soit x réel. E(x) et V(x) sont-elles des fonctions continues en O ? Justifier. La composante normale du champ subit une discontinuité à la traversée du disque chargé ; le potentiel est une fonction continue.  On considère deux disques D1 et D2, de même rayon R, chargés en surface. D1 est centré en O1 tel que xO1 = -½a et porte la densité -s. D2 est centré en O2 tel que xO2= +½a et porte la densité +s. Montrer que pour x >>a et x >>R, la distribution est équivalente à un dipôle électrostatique placé en O. 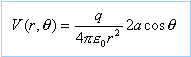Le potentiel crée par le dipole en M est : utiliser le théorème d'Al Kashi dans les triangles OBM et OAM en remarquant que cos q=- cos (p-q) r1²= a²+ r²-2arcosq r2²= a²+ r²+2arcosq mettre r² en facteur commun et effectuer un développement limité au premier ordre expression du gradient en coordonnées polaires   Montrer que le moment dipolaire de la distribution formée par les deux disques vaut : p =pR2 s a ux. On appelle dipôle électrostatique l'ensemble de deux charges ponctuelles opposées situées à une distance "a" l'une de l'autre. La distance "a " reste petite par rapport à la distance où l'on étudie les effets des deux charges. On appelle moment dipolaire, le vecteur p. dans ce cas Q = pR2 s. 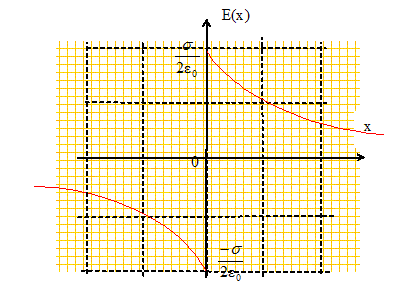Exprimer E(z) pour un point M de l'axe dans le cas de cette approximation dipolaire. dans les expressions ci-dessus remplacer l'angle q par la valeur zéro. Retrouver cette expression à partir d'un développement limité. Plan infini portant une charge surfacique . s>0 : charge surfacique.  Montrer qu'en tout point de l'axe, défini par OM =x ( x >0) , le champ E s'écrit : E(M) = s 2e0 ux La distribution de charge est invariante par translation suivant Ox : le champ ne dépend pas de la variable x. 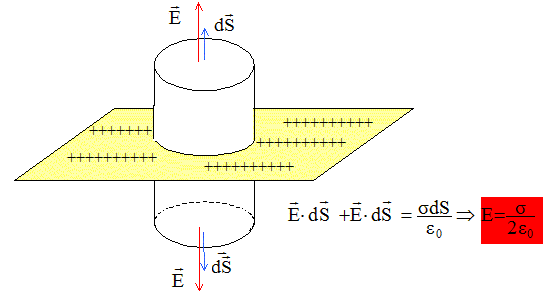La distribution de charge est invariante par translation suivant Oy : le champ ne dépend pas de la variable y. La distribution de charge est invariante par translation suivant Oz : le champ ne dépend pas de la variable z. La distribution de charge est invariante par rotation de l'axe Oz : le champ ne dépend pas de l'angle q. Le champ électrostatique ne dépend pas des variables x, y et z. Tout plan contenant l'axe Oz est plan de symétrie pour la distribution de charge : le champ électrostatique est donc porté par l'axe Oz. Appliquer le théorème de Gauss : la surface de Gauss est un cylindre de section dS. Le flux du champ est nul à travers la surface latérale du cylindre, celle-ci étant perpendiculaire au champ. 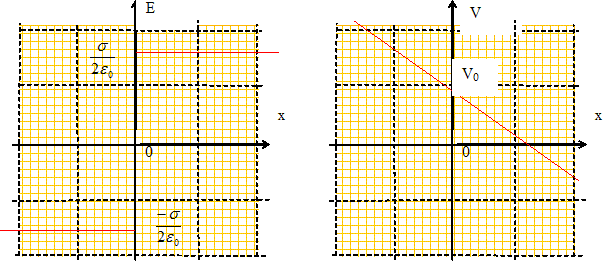Que valent E(0) et E(x<0). Le champ subit une discontinuité à la traversée du plan. Etablir l'expression du potentiel V(x).  Rechercher une primitive de E ( E= - grad V) : on note V0 le potentiel du plan. V = V0 - s x 2e0 Tracer E(x) et V(x) quel que soit x réel. On étudie à présent la distribution constituée de deux plans infinis parallèles perpendiculaires à l'axe x. L'un portant la charge surfacique -s, placé en 01, l'autre portant la charge surfacique +s, placé en O2. Cet ensemble définit un condensateur plan, dont les plans sont les armatures. Calculer U =V(02) - V(OI). On déduit le potentiel par intégration ( E= - grad V). V(O2) = V0 - s x(O2) e0 ; V(O1) = V0 - s x(O1) e0 ; U = V(O2) -V(O1) = s [x(O1)-x(O2)] e0 Sachant que «Q = CU », calculer C, la capacité du condensateur par unité de surface des armatures, en fonction de a et de e0. a = x(O1)-x(O2) ; Q = s , charge par unité de surface. C = Q U = s e0 s a ; C = e0 a L'unité du Système international pour e0 est le« Farad. métre-l.». Commenter. La capacité par unité de surface est d'autant plus grande que les plaques sont plus proches ( a plus petit). Mais en rapprochant les plaques, il ne faut pas trop augmenter U, car il y a un risque de "claquage" du condensateur. Cette distribution peut-elle être assimilée à un dipôle électrostatique? Justifier. Non : un dipôle électrostatique est l'ensemble de deux charges ponctuelles opposées, situées à une distance a l'une de l'autre. Un plan infini chargé ne peut pas être assimilé à une charge ponctuelle. Les condensateurs réels ont des dimensions finies. En quoi l'hypothèse «plan infini» simplifie-t-elle le calcul ? On peut utiliser les symétries ( voir ci-dessus).

retour -menu