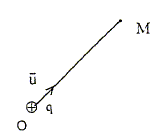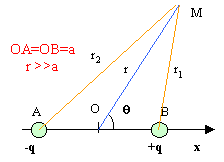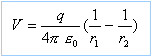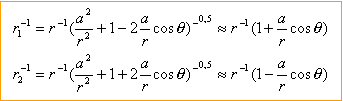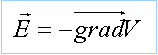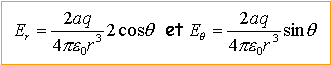Electrostatique : dipôle dans un champ extérieur uniforme Concours ITPE 2002.

Les vecteurs sont écrits en gras et en bleu. On étudie deux distributions de charges électriques et leurs interactions avec un champ électrique extérieur. On note e0 la permitivité diélectrique du vide. La distribution D1 est une charge ponctuelle q située en O. Soit un point M situé à la distance r de O et u un vecteur unitaire porté par OM et dirigé de O vers M. Donner le champ électrique E(M) et le potentiel électrique V(M) crées en M par cette charge. E(M) = 1 4 p e0 q r2 u Si q est positif E(M) et u ont le même sens. 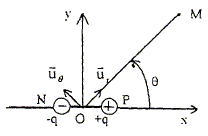Si q est négatif E(M) et u sont de sens contraire V(M) = 1 4 p e0 q r + Constante La distribution D2 est un dipôle électrique rigide constitué de deux charges ponctuelles +q située en P ( avec q >0 ) et -q située en N. Les points P et N sont situés sur l'axe Ox, symétriquement par rapport au point O, avec OP=ON=a. Soit p = q NP le moment dipolaire du dipôle, de norme p. Un point M appartenant au plan xOy est repèré par ces coordonnées polaires r = OM et q =(p, OM). Soit ( ur et uq ) la base associée aux coordonnées polaires. On se place dans le cas ou r >>a. Déterminer le potentiel électrique V(M) = V(r,q) crée en M par le dipôle en fonction de e0, r, p et q en se limitant au terme en 1/r2.     Le potentiel crée par le dipole en M est : utiliser le théorème d'Al Kashi dans les triangles OBM et OAM en remarquant que cos q=- cos (p-q) r1²= a²+ r²-2arcosq r2²= a²+ r²+2arcosq mettre r² en facteur commun et effectuer un développement limité au premier ordre 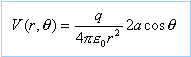avec p = 2a q. En déduire les composantes radiale Er et orthoradiale Eq du champ électrique crée en M par le dipôle. expression du gradient en coordonnées polaires Quelle remarque peut-on faire en comparant les champs crées par D1 et D2 ? Le champ crée par D1 est proportionnelle à 1/r2 ; celui crée par D2 est proportionnel à 1/r3. 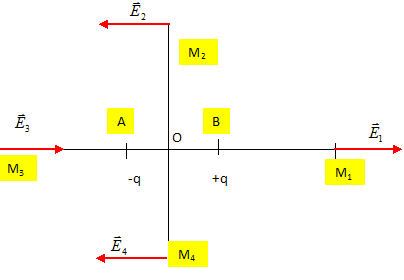Préciser sur un schéma la direction du champ électrique pour quelques points particuliers M1, M2, M3 et M4 situés à égale distance de O et d'angles polaires respectifs égaux à 0, ½p, p et 3p/2. 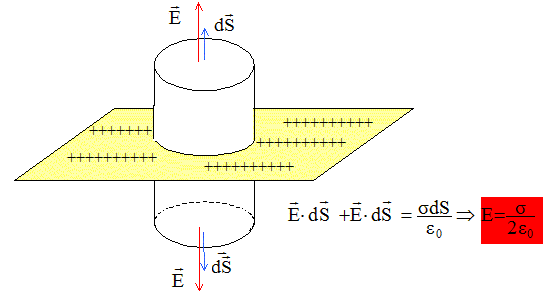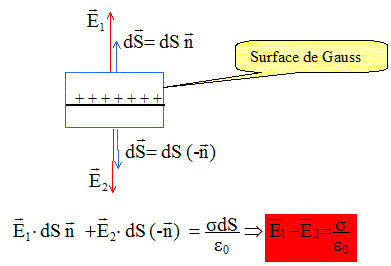angle polaire Er Eq direction du champ M1 0 4aq 4p e0r3 0 radiale M2 90° 0 2aq 4p e0r3 orthoradiale M3 180° - 4aq 4p e0r3 0 radiale, dirigé vers O M4 270 0 -2aq 4p e0r3 orthoradiale Dans une région de l'espace où règne un champ électrique uniforme E0 on place D1 ou D2 et on étudie l'interaction de ces distributions avec ce champ extérieur. Le champ  E0 est crée par un condensateur plan formé par deux plaques parallèles planes A et B. Les plaques sont assimilables à des plans infinis, d'équations x=-a et x= a, chargés uniformément en surface avec des densités surfaciques de charge s (s positif pour A et -s pour B). Montrer que le champ crée entre les deux plaques est uniforme et calculer sa valeur en fonction de a et e0. La distribution de charge est invariante par translation suivant Ox : le champ ne dépend pas de la variable x. La distribution de charge est invariante par translation suivant Oy : le champ ne dépend pas de la variable y. La distribution de charge est invariante par translation suivant Oz : le champ ne dépend pas de la variable z. La distribution de charge est invariante par rotation de l'axe Oz : le champ ne dépend pas de l'angle q. Le champ électrostatique ne dépend pas des variables x, y et z. Tout plan contenant l'axe Oz est plan de symétrie pour la distribution de charge : le champ électrostatique est donc porté par l'axe Oz. Appliquer le théorème de Gauss : la surface de Gauss est un cylindre de section dS. Le flux du champ est nul à travers la surface latérale du cylindre, celle-ci étant perpendiculaire au champ. Que valent E(0) et E(x<0). Le champ subit une discontinuité à la traversée du plan. 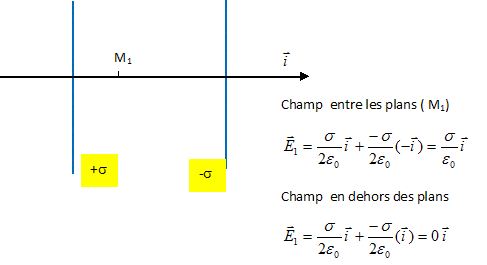E(M) = s 2e0 ux On place D1 au point O. Quelle est l'action subie par la charge q placée en O ? Quel mouvement en résulte t-il ? Cette charge q est soumise à la force F= qE0. Sous l'action de cette force, la charge est animé d'un mouvement rectiligne uniformément accéléré jusqu'à la plaque négative ( si q>0). Le potentiel électrique au point O est égal à V0. Exprimer l'énergie potentielle U d'interaction de q dans le champ électrique. U= q V0. On place D2 au point O. Le dipôle rigide de moment dipolaire p fait un angle a avec E0. Quelle est l'action subie par le dipôle ? Quel mouvement en résulte t-il ? Quelles sont les valeurs de a qui correspondent à des positions d'équilibre du dipôle ? Préciser la stabilité de ces positions. Le dipôle est soumis à un couple de forces de moment C = p^ E0. Sous l'action de ce couple de forces, le dipôle tourne et s'aligne avec le champ extérieur. Les positions d'équilibre du dipôle correspondent à la valeur zéro du moment du couple : équilibre stable : a=0, p colinéaire et de même sens que E0. équilibre instable : a=180°, p colinéaire et de sens contraire à E0. Exprimer l'énergie potentielle U d'interaction du dipôle dans ce champ extérieur en fonction de p et E0. On note V le potentiel en A et V+dV le potentiel en B. L'énergie du dipôle est : U = -qV +q(V+dV = qdV La distance AB étant très faible : dV = - E0. AB, d'où : U = -q E0. AB Or le moment dipolaire p est égal à : q AB d'où : U = -p.E0

retour -menu