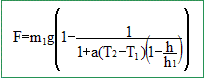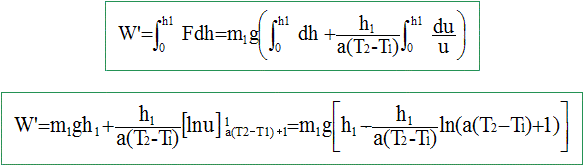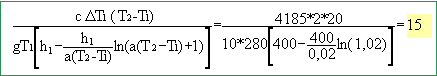énergie thermique des mers (ETM) ; pompe à chaleur concours ITPE 2002

Une centrale thermique expérimentale, dans une zone tropicale, utilise comme source chaude (SC) l'eau de la surface de l'océan et comme source froide (SF) l'eau prise en profondeur. On considère que l'eau de surface est à t2 = 27 °C et que l'eau en profondeur est à t1 = 7°C. On s'intéresse au rendement théorique d'une telle machine. Au cours d'un cycle, le fluide échange avec le milieu extérieur Q2 avec la SC, Q1 avec SF et un travail W. Déduire l'expression du travail |W| en fonction de |Q1|, T2 et T1. La variation d'énergie interne est nulle au cours du cycle DU=0 = W+Q1+ Q2 =0 soit W = -Q1- Q2 . Le rendement théorique maximum correpond à la réversibilité. La variation d'entropie est nulle au cours du cycle : DS=0 = Q1/T1 + Q2/T2. Q2 = -Q1T2/T1. par suit W = -Q1 + Q1T2/T1 = Q1 ( T2/T1-1) Or T2 > T1 et Q1<0 d'où |W| = |Q1|( T2/T1-1). L'eau chaude étant gratuite, le coût essentiel du fonctionnement provient du travail qu'il faut fournir pour pomper l'eau froide. Le maintient d'une température de la SF rigoureusement constante nécessiterait le pompage d'une quantité infinie d'eau à chaque cycle. On tolère une variation DT1= 2 K de la température de la source froide. Donner dans ces conditions, l'expression de |Q1|. |Q1| = m1 c DT1. par suite |W| = m1 c DT1 ( T2/T1-1) = m1 c DT1 ( T2-T1)/T1. On donne la masse m1 d'eau froide qu'il faut pomper à chaque cycle et la chaleur massique de l'eau c = 4185 J K-1 kg-1. Déterminer l'expression de la poussée d'Archimède s'exerçant sur une masse m d'eau à T1, plongée dans l'eau à T, en fonction de la masse m et des masses volumiques de l'eau r(T1 ) et r(T). On note V le volume de cette masse m d'eau : m = Vr(T1) La poussée d'Archimède est égale au poids du volume de fluide déplacé : P = Vg r(T) = m g r(T) / r(T1). En déduire l'expression de la force qu'il faut exercer sur cette masse d'eau pour la maintenir à l'équilibre.  valeur de cette force = |poids - poussée |; F =| mg -m g r(T) / r(T1)|. F = mg | 1-r(T) / r(T1)|. On considère que la masse volumique de l'eau est donnée par la relation : r(T)= r(T1)/ [1+a(T-T1)] avec T = T2-bh et b = (T2-T1)/h1 ; h1 = 400 m, profondeur à laquelle l'eau est pompée. Calculer le travail W' qu'il faut fournir pour amener la masse d'eau m1, de la profondeur h1( température T1) à la surface ( température T2). On suppose que la température de l'eau pompée ne varie pas. F = m1g | 1-r(T) / r(T1)| et r(T)= r(T1)/ [1+a(T-T1)] et T = T2-bh F = m1g | 1-1 / [1+a(T-T1)] | = m1g | 1-1 / [1+a( T2-bh -T1)] | travail élémentaire dW = Fdh, puis intégrer entre 0 et h1 : on pose : u = 1+a(T2-T1) ( 1-h/h1) ; du = -a(T2-T1) dh / h1 ; dh = -h1 /(a(T2-T1)) du. Calculer le rendement ( efficacité) |W/W'| de la centrale. g= 10 m/s2 et a = 10-3 S.I.    On souhaite maintenir la température d'un local à la température Tc=293 K alors que celle de l'extérieur est Tf= 273 K. Pour cela on doit fournir au local la puissance thermique F=12 kW. On désire comparer différents systèmes de chauffage. On chauffe directement le local en utilisant du bois comme combustible. Déterminer la masse de bois mB consommée par heure. Energie ( J) = puissance (W) * durée (s) Energie = 12000*3600 = 4,32 107 = 43,2 MJ La combustion d'un kilogramme de bois fournit 18 MJ.  mB =43,2/18 = 2,4 kg. 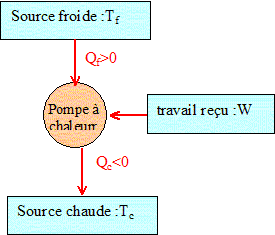On utilise une pompe à chaleur fonctionnant réversiblement. Etablir l'expression de l'efficacité et la calculer. En déduire la puissance mécanique du moteur de la pompe.   premier principe : W+Qf+Qc = 0 sur le cycle. second principe : Qf/Tf+Qc/Tc <= 0 sur le cycle. d'où : -(W+Qc)/Tf+Qc/Tc <= 0 ; Qc[ 1//Tc -1/Tf]<=W/Tf Or Qf est positif, le fluide doit retirer de la chaleur à la source froide ; de plus : Tf<Tc, l'expression entre crochets est positive. Donc W est positif et Qc est négative. coefficient d’efficacité , notée e, ( réversibilité) : gain / dépense =| chaleur cédée au local |divisée par le travail reçu.  e = -Qc/W <=Tc/(Tc-Tf)/=293/20=14,65 Puissance mécanique du moteur de la pompe : 12000 / 14,65 = 819 W. 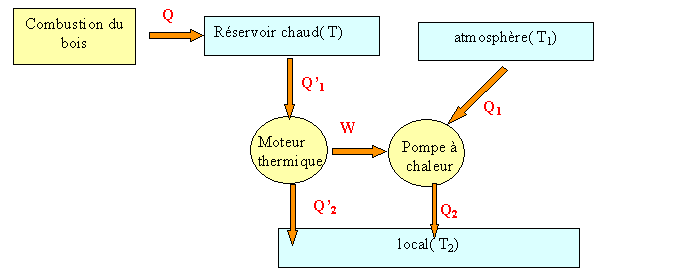On imagine maintenant que le bois est utilisé pour maintenir la température T= 573 K d'un réservoir qui sert de source chaude à un moteur dont la source froide est constituée par l'atmoshère du local. L'énergie mécanique de ce moteur est convertie intégralement en énergie électrique qui est utilisée pour faire fonctionner réversiblement une pompe à chaleur entre l'extérieur et le local. Faire le schéma de l'ensemble de ce système { moteur, pompe, les trois sources }. Préciser le travail et les chaleurs échangés sur le schéma.   Exprimer, en fonction des températures et de la chaleur fournie au moteur thermique par la combustion du bois, la somme des chaleurs reçues par le local. premier principe : pas de variation d'énergie interne du fluide sur un cycle pompe : W+Q1+Q2 = 0 ; moteur : W+Q'1+Q'2 = 0 d'où : Q1 = Q'1+Q'2 -Q2 (1) second principe ( cas de la réversibilité) : la variation d'entropie est nulle sur le cycle. pompe : Q1/T1+Q2/T2 = 0 ; moteur : Q'1/T+Q'2 /T2 = 0 Q2 = Q1T2/ T1 ; Q'2 = Q'1T2/ T ; Q'1 =Q'2 T/T2. (1) s'écrit : Q1 = Q'1+ Q'1 T2/T Q'2-Q1T2/ T1 Q1(1+T2/ T1) = Q'1(1+T2/T) ; Q1 = Q'1(T2+T)T1 / [(T1+T2)T] Q2 = Q1T2/ T1 = Q'1(T2+T)T2 / [(T1+T2)T]  Q2+Q'2 = Q'1(T2+T)T2 / [(T1+T2)T] + Q'1T2/ T  Q2+Q'2 = Q'1T2/ T *[ (T2+T) /(T1+T2) +1]= 43,2 MJ En déduire la masse de bois consommée par heure. Q'1 = 43,2 T /[ T2[ (T2+T) /(T1+T2) +1] ] =43,2*573/[ 293[ (293+573) /(273+293) +1]] Q'1 =  84,48 /(2,53 ) = 33,4 MJ. Dans l'hypothèse où Q = Q'1 alors la masse de bois est : 33,4 / 18 = 1,86 kg. On suppose que la pompe à chaleur utilise comme fluide un gaz parfait auquel on fait décrire un cycle réversible ABCDA formé de 2 isentropiques ( AB et CD) et de 2 isobares ( BC et DA). 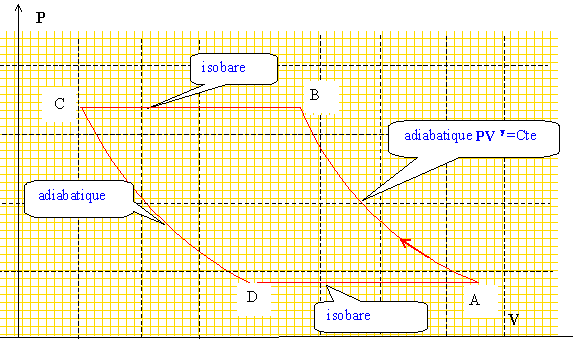PA = 10 bar et TA = 273 K ; PC= 1 bar et TC= 293 K. Donner l'allure du cycle dans le diagramme de Clapeyron.   Calculer l'efficacité du cycle. e = gain ( chaleur cédée au local) / travail investi. Isobare BC : équation d'état du gaz parfait : VB= RTB/PB=RTB/PC. La transformation est réversible : dW= - PdV = -PCdV et WBC= -PC(VC-VB )= PC(VB-VC) ; WBC= R(TB-TC). en utilisant la fonction enthalpie, on trouve, à pression constante : D H=QBC= CP, m (TC-TB). Isobare DA : WDA= R(TD-TA) ; QDA= CP, m (TA-TD). isentropique : travail reçu par un gaz parfait au cours d'une transformation adiabatique réversible : travail élémentaire : dW= -PdV = -Cte /Vg dV=-Cte V-g dV= -Cte/(-g+1) d V-g+1 intégrer entre Vi et Vf : W=-Cte /(-g+1) (Vf-g+1- Vi-g+1 ) avec Cte =PiVig=PfVfg W=-( PfVfg Vf-g+1- PiVig Vi-g+1 ) /(-g+1)= (-PfVf + PiVi) /(-g+1) WAB = (-PBVB+ PAVA) /(-g+1) =R( TA - TB )/(-g+1) ; WCD = (-PDVD+ PCVC) /(-g+1) = R( TC - TD)/(-g+1). La quantité de chaleur reçue au cours d'une transformation adiabatique est nulle. somme des travaux : W = R( TB-TC+TD-TA) g / (g-1). Il faut calculer les températures TB et TD. isentropique CD : g/(1-g) = 1,4/-0,4 =-3,5 : PC TC-3,5 = PD TD-3,5 ; 1/3,5 = 0,286 TD-3,5 = PC TC-3,5/ PD =10 *293-3,5 ; TD=10-0,286 *293 =0,518*293 ; TD= 151,7 K. isentropique AB : PA TA-3,5 = PB TB-3,5 TB-3,5 = PA TA-3,5/ PB = 0,1 *273-3,5 ; TB=0,1-0,286 *273 =1,932*273 ; TB= 527,4 K. W = 8,32(527,4-293+151,3-273)*3,5 = 3,28 kJ. QBC= CP, m (TC-TB)= 29,12*(293-527,4) = -6,83 kJ QDA= CP, m (TA-TD) =29,12*(273-151,7) = 3,53 kJ e = gain ( chaleur cédée au local) / travail investi = 6,83 / 3,28 = 2,1. En supposant que la pompe effectue un cycle par minute, quelle masse faudrait-il pour maintenir le local à 293 K ? M= 29 g/mol ; CP= 29,12 J K-1 mol-1 ; g =1,4.

retour -menu