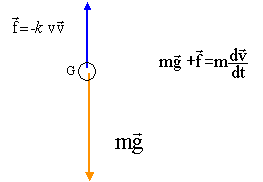Concours manipulateur électroradiologie médicale Toulouse 2007 chute d'un grélon ( Euler) ; solution d'ammoniac

La grêle se forme dans les cumulo-nimbus situés entre 1 000 m et 10 000 m d'altitude où la température est très basse, jusqu'à – 40°C. Le grêlon tombe lorsqu'il n'est plus maintenu au sein du nuage. Au sol sa vitesse peut atteindre 160 km/h.  On étudie un grêlon de masse 13 g qui tombe d'un point O d'altitude 1 500 m sans vitesse initiale. Il peut être assimilé à une sphère de diamètre 3,0 cm. Le point O sera pris comme origine d'un axe Oz orienté positivement vers le bas. L'intensité de la pesanteur sera considérée comme constante et de valeur g0 = 9,80 m.s-2 . Données : volume d'une sphère V = 4/3 p.r3 ; masse volumique de l'air r = 1,3 kg.m-3 .  A ) Chute libre : On admettra que le grêlon tombe en chute libre. Préciser le référentiel d'étude. Que signifie l'expression tomber en chute libre ? Référentiel terrestre supposé galiléen. La chute est dite "libre" lorsque l'objet n'est soumis qu'à son poids. Rappeler les conditions initiales du mouvement du grélon. Vitesse initiale nulle ; la position initiale du grêlon est choisie comme origine de l'axe verticale descendant. En appliquant la deuxième loi de Newton, déterminer les équations horaires donnant la vitesse et la position du centre d'inertie G du grêlon en fonction de la durée t de chute. En chute libre, le poids est la seule force appliquée : ma = mg d'où a=g. La vitesse est une primitive de l'accélération : v= gt ( vitesse initiale nulle) La position est une primitive de la vitesse : z= ½gt².( position initiale prise comme origine) Calculer la valeur de la vitesse lorsqu'il atteint le sol, ce résultat est-il vraisemblable ? Justifier. Au sol z = 1500 m ; t²= 3000/g ; t = [3000/g]½. Repport dans l'expression de la vitesse : v = g[3000/g]½ = [3000*g]½ = [3000*9,8]½ = 171,5 m/s=617 km/h. Cette valeur est bien trop grande pour correspondre à la réalité , ainsi qu'à la valeur proposée dans le texte; on a négligé les forces de frottements sur les couches d'air.   B ) Chute réelle : En réalité le grêlon est soumis à deux autres forces, la poussée d'Archimède FA et la force de frottement fluide F proportionnelle au carré de la vitesse telle que F = K.v2 . Par une analyse dimensionnelle, déterminer l'unité du coefficient K dans le Système International. F : force ( newton) = Masse * accélération soit [M][L][T]-2 ; vitesse ² = longueur ² / temps² soit [L]2[T]-2 ; K= F/v² soit [M][L][T]-2 [L]-2[T]2 = [M][L]-1 L'unité du coefficient K dans le Système International est donc kg.m-1. Donner l'expression de la valeur de la poussée d'Archimède; la calculer et la comparer à celle du poids. Conclure. Poussée d'Archimède = poids du volume de fluide (air) déplacé = volume grêlon * rair*g FA= 4/3 p.r3 rairg avec r = 1,5 10-2 m. FA= 4/3*3,14*(1,5 10-2)3*1,3*9,8 = 1,8 10-4 N. poids P=mg= 0,013*9,8 = 0,13 N La poussée d'Archimède est négligeable devant le poids du grêlon.On néglige la poussée d'Archimède. Représenter sur un schéma( sans échelle) les forces qui s'exercent sur le grêlon. Etablir l'équation différentielle du mouvement. Montrer qu'elle peut s'écrire sous la forme dv/dt = A – B.v2 Ecrire la seconde loi de Newton dans un référentiel terrestre supposé galiléen, suivant un axe vertical descendant. Le grêlon est soumis à son poids, vertical vers le bas et à la force de frottement verticale vers le haut. mg - Kv² = ma = m dv/dt soit dv/dt = g-K/mv². A = g et B= K/m.   On veut résoudre cette équation différentielle par une méthode numérique : la méthode d'Euler. Le tableau suivant est un extrait d'une feuille de calcul des valeurs de la vitesse (v) et de l'accélération (a) en fonction du temps (t). Il correspond aux valeurs : A = 9,80 m.s-2 et B = 1,56.10-2 m-1 , pas de variation Dt = 0,5 s. t(s) v(m/s) a (m/s²) 0 0 9,8 0,5 4,9 9,43 1 9,61 8,36 1,5 13,8 6,83 2 17,2 a4 2,5 v5 3,69 3 21,6 2,49 Déterminer a4 et v5 en détaillant les calculs. 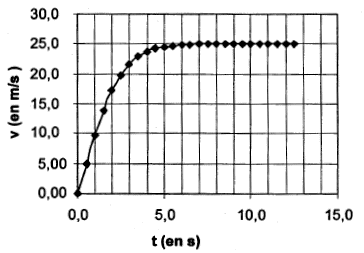On utilise l'équation différentielle pour déterminer a4 : a4 = 9,8-1,56 10-2 v42 avec v4 = 17,2 m/s. a4 = 9,8-1,56 10-2* 17,22 = 5,18 m/s². Dans la méthode d'Euler, on utilise l'approximation suivante : a = Dv / D t. Dv = v5-v4= a4D t soit v5= v4+ a4D t v5= 17,2 + 5,18 * 0,5 = 19,8 m/s. Exprimer la vitesse limite atteinte par le grêlon en fonction de A et B puis calculer sa valeur numérique. Lorsque la vitesse limite est atteinte par le grêlon, la vitesse est constante, l'accélération a est alors nulle. 0= A-Bvl2 soit vl =(A/B)½= (9,8/1,56 10-2)½=25,1 m/s. - La courbe d'évolution de la vitesse en fonction du temps est donnée ci-dessous.   Retrouver graphiquement la valeur de la vitesse calculée au paragraphe précédent. D'après la courbe, l'asymptote horizontale donne la valeur de la vitesse limite, valeur en accord avec celle calculée ci-dessus. L'ammoniac. L'ammoniac NH3 est un gaz qui dissout dans l'eau donne une solution basique d'ammoniaque. Des solutions d'ammoniaque sont vendues dans le commerce. Ces solutions après dilution, sont utilisées comme produit nettoyant et détachant. On se propose d'étudier quelques propriétés de l'ammoniac dissout puis de déterminer sa concentration dans un de ces produits. Données : masse molaire de l'ammoniac : 17g/mol ; couple acide base NH4+ / NH3 : Ka1 = 6,3 10-10. I. NH3(aq) : L'ammoniac est une base en solution aqueuse. Donner la définition d'une base selon Brönsted. base : espèce, ion ou molécule susceptible de gagner un proton H+. Ecrire l'équation de la réaction entre l'ammoniac et l'eau. NH3 + H2O = NH4+ + HO-. Exprimer puis calculer la constante d'équilibre de cette réaction. K = [NH4+]éq[HO-]éq / [NH3 ]éq Or Ka1 = [NH3 ]éq[H3O+]éq / [NH4+]éq et Ke = [HO-]éq[H3O+]éq = 10-14 à 25°C  K = [NH4+]éq[H3O+]éq [HO-]éq / [NH3 ]éq[H3O+]éq= Ke / Ka1 =10-14 /6,3 10-10= 1,59 10-5. On dissout dans un volume d'eau V=250 mL une quantité de matière n d'ammoniac égale à 2,5 10-3 mol. Le pH de la solution S obtenue vaut 10,6. Calculer la concentration c en soluté apporté. concentration c en soluté apporté : c= n/V = 2,5 10-3 / 0,25 = 0,01 mol/L. Calculer la concentration en ion oxonium H3O+ dans la solution.  concentration en ion oxonium H3O+ dans la solution : [H3O+]= 10-pH = 10-10,6 = 2,51 10-11 mol/L En déduire la concentration en ion hydroxyde HO- dans la solution.  concentration en ion hydroxyde HO- dans la solution : [HO-]= 10-14 / [H3O+]= 10-14 / 2,51 10-11 = 4 10-4 mol/L. Montrer que le taux d'avancement final t peut s'écrire t= [HO-]f / c puis le calculer. - Que peut-on dire de la transformation ? avancement (mol) NH3 + H2O = NH4+ + HO- initial 0 n= 2,5 10-3 solvant en grand excès 0 0 en cours x 2,5 10-3 -x x x fin xf 2,5 10-3 -xf xf xf xmax 2,5 10-3 -xmax xmax xmax 2,5 10-3 -xmax = 0 soit xmax =2,5 10-3 mol = n= C V xf = [HO-]f *V = 4 10-4 *0,25 = 10-4 mol/L t= xf / xmax = [HO-]f *V / (CV) = [HO-]f / C = 10-4 / 2,5 10-3 = 0,04. t <<1 en conséquence, la transformation est très limitée. 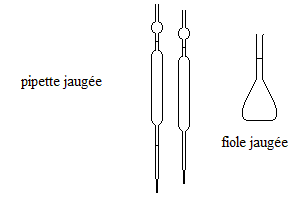Détermination de la concentration en ammoniac de la solution commerciale : Dilution de la solution commerciale. Afin de déterminer la concentration c0 de la solution commerciale, on propose de réaliser un titrage acido-basique de la solution commerciale. Celle-ci étant très concentrée, on fabrique par dilution, une solution S1 de concentration c1 mille fois plus petite. Décrire le protocole expérimntal pour réaliser cette dilution. facteur de dilution = 1000 = volume fiole jaugée (mL)/ volume pipette jaugée(mL). Prélever un mL de la solution mère à l'aide d'une pipette jaugée de 1 mL + pipeteur. Verser dans la fiole jaugée de 1 L puis compléter avec une pissette d'eau distillée jusqu'au trait de jauge. Agiter pour rendre homogène. Titrage acido-basique : on réalise un titrage pH-métrique de v1 = 20,0 mL de solution S1 par une solution d'acide chlorhydrique (H3O+ ; Cl-) de concentration cA= 1,50 10-2 mol/L. L'équation support du titrage est : NH3 + H3O+ = H2O + NH4+. Pour obtenir l'équivalence il faut verser un volume VE = 14,3 mL d'acide chlorhydrique. On note que le pH à l'équivalence vaut 5,7. Définir l'équivalence d'un titrage. A l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoéchiométriques. Etablir la relation à l'équivalence entre c1, V1, cA et VE. - En déduire c1 puis c0. d'après les coefficients de l'équation : n(NH3) équi = n( H3O+) équi soit c1V1= cAVE. c1= cAVE/V1=1,5 10-2 *14,3 / 20 = 1,07 10-2 mol/L. en conséquence c0 = 1000 c1 = 10,7 mol/L Parmi les indicateurs colorés suivants, choisir en justifiant, celui qui pourrait être utilisé pour réaliser ce titrage de façon colorimétrique. indicateur coloré couleur forme acide zonne de virage couleur forme basique hélianthine rouge 3,1 - 4,4 jaune rouge de chlorophénol jaune 5,2 - 6,8 rouge bleu de bromothymol jaune 6,0 - 7,6 bleu phénolphtaléine incolore 8,2 - 10 rose La zone de virage de l'indicateur coloré doit contenir le pH de l'équivalence : le rouge de chlorophénol convient.

retour -menu