Autour de la pression : Bernoulli, Toricelli, Venturi concours technicien laboratoire 2008

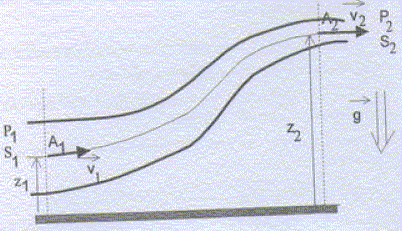
Notion de pression : Un opérateur exerce uniformément et normalement à une surface S une force F. Définir la pression p en un point de cette surface. pression ( Pa) = force (N) / surface (m2). p = F/S. Quelle est l'unité légale de la pression ? pascal (Pa). Justifier rapidement pourquoi : - un char d'assaut est muni de chenilles ; - une punaise a une pointe fine. Un char d'assaut, véhicule lourd, ne doit pas s'enliser dans le sol, sous peine de ne plus pouvoir se déplacer. En augmentant la surface de contact chenilles-sol, on fait diminuer la pression exercée par le véhicule sur le sol : le risque d'enlisement est alors faible. Une punaise doit exercer une pression élevée sur le matériau afin qu'elle puisse s'y planter : la pointe de la punaise doit donc être très fine.  Ecoulement permanent d'un fluide incompressible : On conidère une veine de fluide parfait incompressible de masse volumique m en écoulement permanent et adiabatique dans le champ de pesanteur g. Le fluide pénètre en A1 situé à l'altitude z1, à la pression p1, animé de la vitesse v1 et ressort en A2 situé à l'altitude z2, à la pression p2, animé de la vitesse v2. Les sections de la veine en A1 et en A2 sont respectivement S1 et S2. On suppose que les vitesses sont uniformes à la traverse des sections. On montre que sur une ligne de courant, on peut écrire : ½mv12 +mgz1 +p1 = ½mv22 +mgz2 +p2, ce qui constitue le théorème de Bernoulli.   Que traduit physiquement ce théorème ? Identifier les contributions des différents termes.interprétation énergétique de cette relation : Le théorème de Bernoulli traduit la conservation de l'énergie le long d'une ligne de courant. ½mv12 : énergie cinétique par unité de volume ou densité d'énergie cinétique mgz1 : densité d'énergie potentielle de gravitation p1 : densité d'énergie élastique. Le fluide étant incompressible, montrer que le débit volumique défini par Qv = dV/dt s'écrit : Qv = S1 v1 = S2 v2. Soit un élément de volume dV autour d'un point M ; sa masse est notée dm = d(mv) = constante avec v: vecteur vitesse ; m : masse volumique. d(mv) = constante traduit le fait qu'il n'y a pas d'accroissement de matière autour du point M. dV ( volume) = section * déplacement ; dV = S dx ; dx/dt est une vitesse d'où dV/dt = S v. Le débit volumique (m3 s-1) est donc une section (m2) fois une vitesse (m s-1). Par suite Qv = S1 v1 = S2 v2. Mesure de pressions. Que mesure un manomètre, un bromètre ? Le manomètre mesure la pression d'un gaz ; un baromètre mesure la pression atmosphérique. Le baromètre de Toricelli est constitué d'un tube de verre bouché à une extrémité, rempli de mercure de masse volumique mHg. On retourne le tube sur une cuve à mercure comme l'indique la figure ci-dessous. L'ensemble est placé à la surface terrestre en un lieu où la pression atmosphérique est P0. Déterminer l'expression de P0 en fonction de mHg, g, H et Psat, pression de vapeur saturante du mercure. Dans un liquide homogène, la pression est la même en tout point d'un plan horizontal ; on considère deux points situés dans le plan de la surface libre du mercure, l'un sur la surface en contact avec l'atmosphère, l'autre à l'intérieur du tube. P0 = Psat + mHggH. Déterminer H à la température de 20°C si P0 = 1015 hPa. Psat = 0,26 Pa à 20°C ; mHg= 13,5 103 kg m-3 ; g = 9,81 m s-2 ; P0 = 1,015 105 Pa. H =( P0-Psat) / (mHgg )= (1,015 105 -0,26) / (13,5 103 *9,81)= 0,766 m.   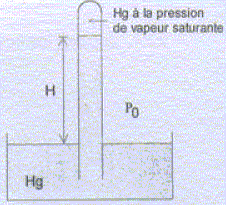Quelle est, sous la pression tmosphérique P0 = 1015 hPa, la force exercée par l'atmosphère sur une surface de 10 cm2. F = P0 S avec P0 = 1,015 105 Pa et S = 10-3 m2. F = 1,015 105 * 10-3 = 101,5 ~101 N. On peut mettre en évidence cette force en réalisant un vide partiel dans un récipient déformable : ce dernier à tendance à s'écraser. On désire refaire l'expérience de Toricelli avec de l'eau. On donne la pression de vapeur saturante de l'eau à 20°C Psat eau =2337 Pa. Calculer la nouvelle hauteur H H =( P0-Psat eau) / (meaug )= (1,015 105 -2337) / ( 103 *9,81)= 10,1 m. L'expérience est difficile à réaliser dans ce cas. Justifier pourquoi l'xpérience de Toricelli est interdite dans les établissements scolaires. Le mercure est toxique par inhalation, contact avec la peau. Lors de l'évaporation de ce liquide à 20°C, une contamination dangereuse de l'air est rapidement atteinte, la limite d'exposition étant 0,025 mg m-3. 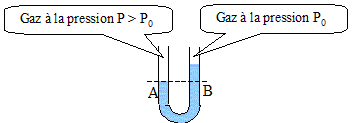On considère un tube en U renfermant un liquide au repos, incompressible, de masse volumique m dans le champ de pesanteur terrestre. Le liquide de chaque branche est en contact avec un gaz. Montrer que si la pression du gaz est la même dans les deux branches du tube, la dénivellation est nulle. Branche de gauche : la pression à la surface libre du liquide est égale à la pression du gaz surmontant le liquide. Branche de droite : la pression à la surface libre du liquide est égale à la pression du gaz surmontant le liquide. Les gaz étant à la même pression, la pression est la même dans le liquide, à la surface libre, dans chaque branche : les surfaces libres de ce liquide homogène sont donc dans un même plan horizontal. Montrer que, si la pression P du gaz à gauche est supérieure à celle P0 du gaz à droite, alors P = P0 +mgh avec h, dénivellation du liquide. 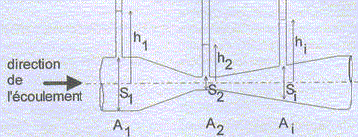Branche de gauche : la pression à la surface libre du liquide vaut P. Dans la branche de droite, la pression en B vaut P0+mgh. A et B étant dans un même liquide homogène et dans le même plan horizontal, on en déduit : P =P0+mgh. La dénivellation h est proportionnelle à la différence de pression P-P0. On considère maintenant l'écoulement permanent adiabatique d'un fluide incompressile dans une conduite présentant un étranglement ( tube de Venturi ). A la verticale des différents points A1, A2... situés aux centres des sections S1, S2...., on dispose de tubes verticaux permettant de mesurer la pression au sein du liquide par la hauteur de celui-ci. Justifier les égalités : S1 v1 = S2 v2 =....SnVn=Qv. vi étant les vitesses aux différents points. Conservation du débit volumique. v12/(2g) + h1 =v22/(2g) + h2 =.....=vn2/(2g) + hn. Ecrire le thorème de bernoulli en remarquant que les points A1, A2, ... An sont tous dans le même plan horizontal (z1=z2=...=zn ). ½mv12 +mgz1 +p1 = ½mv22 +mgz2 +p2 =....=½mvn2 +mgzn +pn. Diviser chaque terme par mg : ½v12 /g + z1 +p1 /(mg)= ½v22 /g+ z2 +p2/(mg) =....=½vn2 /g + zn +pn/(mg). ½v12 /g + p1 /(mg)= ½v22 /g + p2/(mg) =....=½vn2 /g + pn/(mg). (1) pression en A1 : p1 = patm +mgh1 ; p1 /(mg)=patm /(mg)+h1. De même : p2 /(mg)=patm /(mg)+h2 ; pn /(mg)=patm /(mg)+hn. Repport dans (1) : ½v12 /g +patm /(mg)+h1 = ½v22 /g + patm /(mg)+h2 =....=½vn2 /g + patm /(mg)+hn. Le terme patm /(mg) est commun d'où : v12/(2g) + h1 =v22/(2g) + h2 =.....=vn2/(2g) + hn. Montrer alors que : h1-hn = Qv2 / (2gS12) [ (S1/Sn)2-1]. h1-hn =vn2/(2g)-v12/(2g) = v12 /(2g) [vn2/v12 -1] Or v1 = Qv/S1 et vn = Qv/Sn ; vn2/v12 =(S1/Sn)2 par suite : h1-hn = Qv2 / (2gS12) [ (S1/Sn)2-1]. Les résultats expérimentaux sont donnés dans le tableau ci-dessous : tube h(mm) S1(mm2) (S1/Si)2. A1 247,5 530,9 1,000 A2 228,5 422,7 1,577 A3 140,5 265,9 3,987 A4 6,0 201,1 6,973 A5 26,0 221,7 5,737 A6 112,0 267,9 3,927 A7 150,5 319,2 2,767 A8 176,0 374,6 2,009 A9 193,0 434,8 1,491 Calculer les valeurs de h1-hi et de (S1/Si)2-1. 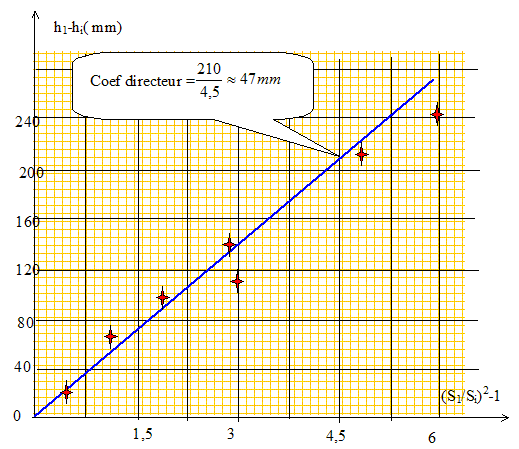i 1 2 3 4 5 6 7 8 9 h1-hi 0 19 107 241,5 221,5 135,5 97 71,5 54,5 (S1/Si)2-1 0 0,577 2,987 5,973 4,737 2,927 1,767 1,009 0,491 Tracer la courbe donnant les variations de h1-hi en fonction de (S1/Si)2-1 et conclure. Certaines mesures expérimentales ne figurent pas sur la droite : le théorème de Bernoulli n'est pas vérifié ; les résultats des mesures font apparaître nettement après le convergent et même avant une perte de charge non négligeable. Donner l'ordre de grandeur du débit volumique ( m3/s). h1-hn = Qv2 / (2gS12) [ (S1/Sn)2-1]. Le coefficient directeur de la droite vaut 0,047 m ; 0,047 = Qv2 / (2gS12) Qv2 = 0,047 (2gS12) ; Qv = (0,047 *2g)½*S1 ; Qv = (0,047 *2*9,81)½*530,9 10-6 = 5,1 10-4 m3/s.

retour -menu