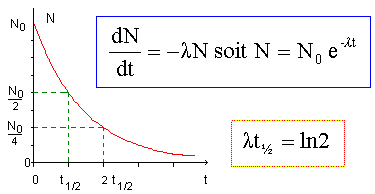flash poto ( RC), radioactivité : technétium 99. Concours manipulateur électroradiologie médicale Poitiers 2008

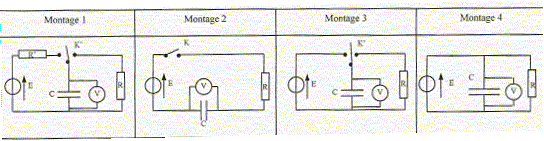
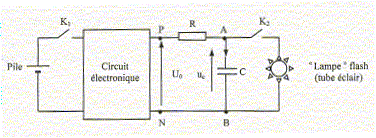
Etude de la charge d'un circuit RC. Quatre montages sont proposés. Seuls deux conviennent pour la charge et la décharge. Indiquer lesquels sans justifier. Montage 1 et montage 3. On désire charge le plus rapidement possible le condensateur. Parmi les deux montages choisis lequel convient le mieux ? Justifier. Montage 3 : la charge est terminée au bout d'une durée voisine de 5 RC ; dans ce montage la résistance du circuit de charge est très faible voir nulle.  Etude de la décharge. Le condensateur de capacité C= 220 mF est chargé sous la tension E=5,0 V. A la date t=0 on débute la décharge dans le résistor de résistance R. Le tableau ci-dessous donne qulesues valeurs de uc à différentes dates : uc(V) 3,2 2,5 1,9 1,0 date t (s) 10,2 15,2 22,0 35,4 A la date t ( constante de temps du circuit) uc est-elle voisine de 93%E ? 37%E ?  37%E. Déduire du tableau la valeur de t. 0,37 E = 0,37*5 =1,85 V ~ 1,9 V. Le tableau indique t = 22 s.  Parmi les expressions proposées ci-dessous, choisir l'expression correcte de la tension uc et l'utiliser pour justifier la réponse précédente.  uc(t) = E exp(t/t) ;  uc(t) = E exp(-t/t) ;  uc(t) = E(1- exp(t/t)). uc(t) = E exp(-1) = 5*0,368 = 1,84 V.   Flash d'un appareil photo. Un flash émet des éclairs intenses et brefs, de durée 1 ms. Son circuit est schématisé ci-dessous ( le circuit électronique permet d'élever la tension de la pile, de sorte que la tension U0 soit égale à 200 V ). La lampe est assimilée à un résistor de résistance r. C= 220 mF et R= 10 kW.   Calculer la durée nécessaire pour charger complètement le condensateur et l'énergie Ec stockée. 5 RC = 5*104*2,2 10-4 = 11 s. Ec =½CU02 =0,5*2,2 10-4 *2002 =1,1*4 = 4,4 J.  Lorsque le photographe appuie sur le déclencheur, l'énergie stockée dans le condensateur est totalement fournie à la lampe pendant la durée de l'éclair. Calculer la puissance moyenne de l'éclair. P(W)= Ec(J)/Dt (s) Dt = 10-3 s ; P = 4,4/10-3 = 4,4 103 W = 4,4 kW. Etablir l'expression littérale de P en fonction de U0 et de r.  La puissance est dissipée sous forme de chaleur dans la lampe : P= rI2 avec U0 = rI P = U02/r. Si on veut que la puissance de l'éclair soit importante, comment faut-il choisir U0 et r ? calculer r. U0 doit être élevée et r doit être faible.  r = U02/P = 2002 / 4,4 103= 9 W.   Radioactivité et imagerie médicale. Pour vérifier le fonctionnement d'un organe, l'imagerie médicale peut être réalisée par une détection externe du rayonnement émis par un produit radioactif injecté. On utilise des radioisotopes émetteurs de rayonnement g ou des émetteurs de positons comme le technétium 99. Partie A. Le technétium 9943Tc se transforme en molybdène 9942Mo par émission b+ ( émission de positon). Ecrire l'équation de la réaction nucléaire en supposant que le noyau fils est dans un état excité. 9943Tc ---> 9942Mo* +01e. Ecrire l'équation de la désexcitation du molybdène revenant à l'état fondamental. 9942Mo*-->9942Mo + 00g.  Quand le positon obtenu rencontre un électron, les deux s'annihilent en produisant deux rayonnements g qui sont détectés. Ecrire l'équation nucléaire de l'annihilation.  01e + 0-1e ---> 2 00g. Pourquoi évite t-on d'utiliser dans l'imagerie médicale, les sources de rayonnement a ou b- : on prendra soins de redéfinir chacun de ces rayonnement. alpha : noyau d'hélium 42He, particule chargée ionisante : étant lourdes et portant une charge électrique, elles sont très facilement arrêtées par la matière environnante. b- :   électron, particule chargée : il est arrêté par la matière et les champs électromagnétiques environnants. Une feuille d’aluminium de quelques millimètres d'épaisseur peut arrêter les électrons. En conséquence ce type de particules ne pourra pas atteindre la gamma-caméra externe. Partie B. Rappeler la loi de désintégration radioactive. Soit un échantillon contenant N0 noyaux radioactifs à la date t0 =0 choisie comme date initiale. Soit N le nombre de noyaux radioactifs (non désintégrés) encore présents dans l'échantillon à la date t. l est la constante radioactive, caractéristique d'un radioélément. On donne l = 3,21 10-5 s-1.  Calculer la demi-vie t½ du technétium. t½ = ln2 / l = ln2 / 3,21 10-5 =2,16 104 s. Déterminer au bout de combien de temps la quantité de substance radioactive injectée dans l'organisme a diminué de 90 %. Il reste 10 % des noyaux initiaux soit N/N0 = 0,1. 0,1 = exp(- 3,21 10-5 t) ; 3,21 10-5 t = - ln0,1 = 2,30 ; t = 2,30/3,21 10-5 = 7,17 104 s.  On veut que l'activité A de la substance administrée pour l'imagerie soit comprise entre 30 et 1000 MBq. Calculer le nombre maximum de noyaux de technétium que doit comporter la source injectée dans l'organisme. A = l N ; N = A/l avec A = 1000 106 Bq = 109 Bq. N = 109 / 3,21 10-5 = 3,11 1013 noyaux.  On néglige la masse des électrons et on considère que la masse molaire des noyaux de technétium est M=99 g/mol. NA = 6,02 1023 mol-1. En déduire la masse maximale de technetium à injecter. Quantité de matière (mol) n = N/NA =  3,11 1013 /6,02 1023 =5,2 10-11 mol masse m = nM = 5,2 10-11*99 =5,1 10-9 g.

retour -menu