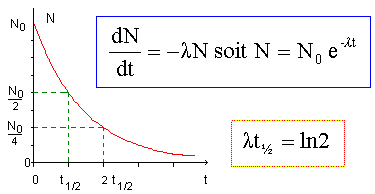Pile alimentant un circuit RLC, radioactivité. Concours manipulateur électroradiologie médicale Nantes 2008

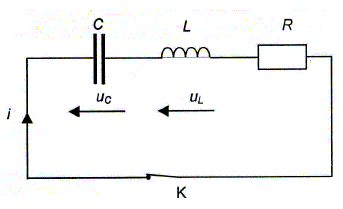
Une pile est composée de deux demi-piles reliées par un pont salin ( gel d'Agar-Agar imbibé d'une solution de nitrate de potassium). La première pile est constituée d'un fil de titane de masse m2 = 1,0 g qui plonge dans V2= 50 mL de nitrate de titane II( Ti2+ + 2NO3-) de concentration apportée en ion titane c2 = [Ti2+]i =3,0 10-2 mol/L. La seconde est constituée d'un fil d'argent de masse m1 = 0,90 g qui plonge dans V1= 50 mL de nitrate de titane II( Ag+ + NO3-) de concentration apportée en ion argent c1 = [Ag+]i =2,0 10-2 mol/L. On associe cette pile à un ampèremètre et une résistance en série. L'ampèremètre indique que le courant circule du fil d'argent vers le fil de titane à l'extérieur de la pile. Préciser, le justifiant la polarité de la pile. Les électrons se déplacent, dans le circuit extérieur, en sens contraire du sens conventionel du courant, c'est à dire du fil de titane vers l'argent. Le titane constitue donc la borne négative de la pile et l'argent la borne positive. Montrer que l'équation d'oxydoréduction de fonctionnement de la pile est : 2Ag+ aq + Ti(s) = Ti2+ aq + 2 Ag (s). (1) Oxydation du titane : Ti(s) = Ti2+ aq + 2e-. Réduction des ions argent : 2Ag+ aq + 2e- = 2 Ag (s). En additionnant ces deux demi-équations on retrouve (1) Quelle est l'électrode appelé cathode. Justifier. A la cathode positive on observe une réduction, gain d'électron : l'argent constitue la cathode. Où se dépose l'argent formé lorsque la pile débite ? L'argent formé se dépose sur le fil d'argent utilisé comme cathode.   La constante d'équilibre associée à l'équation (1) est K= 1,1 1084. Définir et calculer le quotient de réaction initial Qr i du système ainsi constitué. Qr i = [ Ti2+ aq] i / [ Ag+ aq] 2i = c2/c12 =3,0 10-2 / (2,0 10-2 )2 =300/4=75. Dans quel sens va évoluer spontanément le système étudié ? Qr i< K, le système évolue spontanément dans le sens direct. Oscillations électriques dans un circuit RLC série. La pile de f.e.m E=1,0 V a servi à charger le condensateur de capacité C. Pour étudier les conditions d'obtention d'oscillations électriques libres à la fréquence propre f0 = 44 kHz, on réalise le circuit suivant : Un oscilloscope à mémoire permet d'enregistrer la tension aux bornes du condensateur. L'oscillogramme est représenté ci-dessous : La bobine a une inductance de valeur L= 40 mH ; R est la résistance totale du circuit. Le condensateur est initialement chargé sous une tension Uc=1,0 V. A l'instant t=0, on ferme l'interrupteur K. Comment appelle t-on le type de régime observé ? Oscillations électriques libres amorties. Comment peut-on éviter l'amortissement des oscillations, sachant que la résistance du cirrcuit ne peut pas être nulle ? On utilise un dispositif électronique compensant à chaque instant l'énergie perdue par effet Joule dans R. Donner l'expression de la période T0 des oscillations dans le cas où le problème de l'amortissement a été résolu. Préciser les unités des grandeurs intervenant dans cette expression. T0= 2p (LC)½. période en seconde ; inductance L en henry( H) et capacité C en farad (F). Déterminer la capacité C de manière à obtenir des oscillations à la fréquence f0=44 kHz. T0 = 1/f0 = 1/44 103 = 2,27 10-5 s. C = T02 /(4p2L)=( 2,27 10-5)2 / (4*3,142*0,04) =3,3 10-10 F.   Un nouveau cyclotron à Nantes pour mieux lutter contre le cancer. " Aujourd'hui très focalisée sur les cancers, la médecine nucléaire est appelée à élargir son champ d'application, notamment en cardiologie. A cette fin, il est nécessaire de disposer de radio-isotopes variés, en quantités suffisantes et aux caractéristiques adaptées, telles qu'une demi-vie ni très inférieure ni très supérieure à quelques heures. Il faut non seulement que la production de rayonnements reste suffisante le temps de préparer et d'effectuer le diagnostic ou la thérapie mais aussi que les radio-isotopes ne demeurent pas trop longtemps substantiellement actifs une fois leur utilisation achevée. De nouveaux isotopes particulièrement intéressants seront disponibles grâce au cyclotron Arronax. Il s'agit par exemple du cuivre 64, un émetteur de positons utile pour la TEP, du cuivre 67, un émetteur de rayonnement b- pour la radiothérapie vectorisée, ainsi que de l'astate 211, un émetteur de particules a dont l'effet thérapeutique est particulièrement très puissant car ces dernières déposent beaucoup d'énergie dans une zone très restreinte." Extrait de "Tête chercheuses" actualité et culture des sciences en Pays de Loire. Printemps 2008. Définir le terme isotope. Ilmlustrer cette notion par un exemple tiré du texte. Deux isotopes possèdent le même numéro atomique mais des nombres de neutrons différents. 64 Cu et 67Cu. Citer les trois particules émises caractéristiques des radioactivités a, b+, b- ainsi que leur formule. a : noyau d'hélium 4 2He ; b+ positon 01e ; b- électron 0-1e. En vous aidant du texte, écrire l'équation nucléaire relative à la désintégration du cuivre 64. cobalt nickel cuivre zinc gallium bismuth polonium astate radon francium 27Co 28Ni 29Cu 30Zn 31Ga 83Bi 84Po 85At 86Rn 87Fr  6429Cu --> AZX + 01e . Conservation de la charge : 29=Z+1 ; Z = 28 conservation du nombre de nucléons : 64=A+0.  6429Cu -->6428Ni + 01e . En vous aidant du texte, écrire l'équation nucléaire relative à la désintégration du cuivre 67.  6729Cu --> AZX + 0-1e . Conservation de la charge : 29=Z-1 ; Z = 30 conservation du nombre de nucléons : 67=A+0.  6729Cu -->6730Zn + 0-1e . En vous aidant du texte, écrire l'équation nucléaire relative à la désintégration de l'astate 211. 21185At --> AZX + 42He . Conservation de la charge : 85=Z+2 ; Z = 83 conservation du nombre de nucléons : 211=A+4; A = 207  21185At -->20783Bi + 42He. Définir le terme demi-vie. A partir de quel graphe peut-on lire une demi-vie ? La demi-vie radioactive,(ou période) notée T ou t½, d'un échantillon de noyaux radioactifs est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintègrés. A partir du graphe N(t) = f(t) ou A(t) = g(t) ( loi de décroisance radioactive) Démontrer la relation liant la demi-vie t½ à la constante radioactive l d'un élément radioactif. Loi de décroissance radioactive : N(t) = N0 exp(-lt). N(t½) = ½N0 = N0 exp(-lt½) ; 0,5 = exp(-lt½) ; ln 0,5 = -ln 2 = -lt½.

retour -menu