Etude du flash d'un appareil photo concours Orthoptie Nantes 07

Charge du condensateur. Quatre piles de fem E = 1,5 V et de résistance interne r faible, montées en série, permettent, lorsque l'interrupteur K est en position 1, de charger le condensateur. Montrer que q(t) = A+B exp(-t/t). Additivité des tensions : 4E-4ri = q/C avec i = dq/dt. 4E-4rdq/dt=q/C ; dq/dt +1/(4rC) q = E/r (1). On pose t = 4rC. Solution générale de l'équation sans second membre : q=B exp(-t/t) Solution particulière de (1) : q= 4EC. Solution générale de (1) : q = 4EC+B exp(-t/t) Exprimer A et t en fonction de E, C et r. 0 t=0, la charge est nulle d'où : 0 = 4EC+B soit B= -4EC. q(t) = 4EC(1-exp(-t/t). C= 2 F Le constructeur indique que la durée de la charge est de l'ordre de 2s. Donner l'ordre de grandeur de r. La charge est pratiquement terminée à t = 5t d'où t voisin de 2/5 = 0,4 s. t = 4rC avec C= 2 F soit r de l'ordre de : 0,05 W. Exprimer puis calculer l'énergie emmagasinnée par le condensateur au cours de la charge. ½C(4E)2 = 0,5*2*62 =36 J.    Décharge du condensateur. 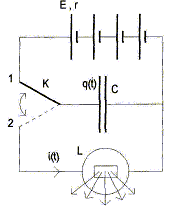La décharge brutale du condensateur dans la lampe, lorsque K bascule en position 2, permet de provoquer un flash. La lampe sera assimilée à une résistance de valeur R, très faible, la puissance dissipée par effet Joule est entièrement transformée en puissance lumineuse. Déterminer l'équation différentielle que doit satisfaire le courant i(t) traversant la lampe. q/C = Ri avec i = -dq/dt ( le courant de décharge a le sens contraire du courant de charge) q/C = Ri : dériver par rapport au temps 1/C dq/dt = R di/dt -i/C =Rdi /dt soit : di/dt + 1/(RC) i = 0. On pose t1 =RC. di/dt + 1/t1 i = 0. (2) Montrer que la solution s'écrit : i(t) = D exp(-t/t1). Solution générale de (2) : i(t) = D exp(-t/t1) A t=0, fermeture de l'interrupteur en position 2, l'intensité valait : i(t=0) = -4E/R. ( tension aux bornes du condensateur chargé : 4E ; changement de sens du courant ; tension aux bornes de R : Ri(t=0) ) Par suite D = -4E/R et i(t) = -4E/R exp(-t/t1). Exprimer la puissance lumineuse PL(t) délivrée par le flash en fonction du temps. " la puissance dissipée par effet Joule est entièrement transformée en puissance lumineuse" PL(t) = R i2 = R [4E/R]2 exp(-2t/t1). PL(t) =16 E2/R exp(-2t/t1). Lors de l'utilisation du flash, le temps d'ouverture du diaphragme de l'appareil photo est imposé par le constructeur et égal à 0,01 s. Justifier pourquoi le constructeur impose un temps de pose et donner un ordre de grandeur de R. Il faut d'abord que le diaphragme soit ouvert avant l'émission du flash, afin que la pellicule soit impressionée dans les meilleurs conditions. L'énergie stockée par le condensateur doit être libérée en un temps très court, 0,01 s. 5 t1 = 0,01 = 5RC avec C= 2 F d'où R = 0,01/10 = 0,001 W. Comparaison éclairement solaire et éclairement lié au flash. Le flash éclaire uniformément une zone conique définie par un angle a=30°. Exprimer la surface totale éclairée S à la distance d= FM en fonction de d et a. On note r le rayon du disque éclairé : tan a = r/d ; r = d tan a. Surface du disque : S = pr2 = pd2 tan2 a. Exprimer l'énergie surfacique moyenne ( J m-2) reçue par la surface éclairée à la distance d. 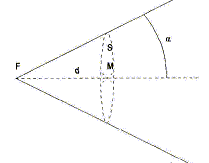Energie stockée par le condensateur : ½C(4E)2 =8CE2. Puis diviser par la surface S : 8CE2 / (pd2 tan2 a). Le temps d'ouverture est égal à 0,01 s ; exprimer la puissance surfacique ou intensité lumineuse I ( W m-2) reçue par la surface éclairée. Diviser l'énergie surfacique par la durée : I = 800CE2 / (pd2 tan2 a).  Le soleil éclaire une surface perpendiculaire à ses rayons avec une intensité lumineuse IS= 1400 W m-2. Calculer la distance d permettant d'obtenir un éclairement comparable à l'éclairement solaire pendant la prise de vue du flash. IS = 800CE2 / (pd2 tan2 a). pd2 tan2 a = 800CE2 /IS ; d2 = 800CE2 /(IS p tan2 a ) ; d = E/tan a [800C/(IS p )]½. d= 1,5 / tan 30 [800*2/(1400*3,14)]½ =1,57 m.

retour -menu