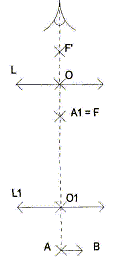Observation d'un petit objet avec une loupe, microscope : réfraction concours Orthoptie Nantes 07

Observation d'un objet AB ( AB = 10-5 m) à l'oeil nu. On place l'oeil à 20 cm de l'objet soit au punctum remotum ( distance minimale permettant la vision nette). Le pouvoir déparateur de l'oeil ( plus petit angle que l'on puisse visualiser) est éagl à 3 10-4 rad. Peut-on séparer les deux points A et B à l'oeil nu ? Justifier par un calcul. Diamètre apparent de AB : tan a voisin de a ( rad) = 10-5 / 0,20 = 5 10-5 rad. valeur inférieure au pouvoir séparateur de l'oeil : A et B sont confondus, inséparables. Observation d'un objet AB ( AB = 10-5 m) avec une loupe.   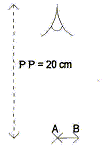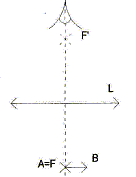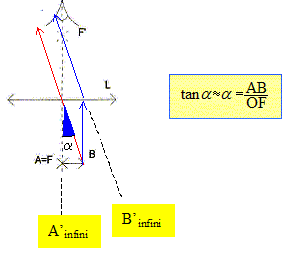Une loupe est une lentille mince convergente de distance focale f'= 5 cm. Pour une observation confortable, on place la loupe telle que son foyer objet F soit confondu avec A. Sous quel angle visualise t-on AB à travers la loupe ? L'utilisation de la loupe permet-elle de séparer A et B ?     . a = 10-5 / 0,05 = 2 10-4 rad. valeur inférieure au pouvoir séparateur de l'oeil : A et B sont confondus, inséparables. 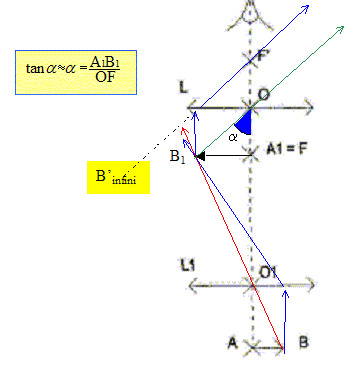Observation d'un objet AB ( AB = 10-5 m) avec un microscope. L'objet AB est placé devant la première lentille L1 ( objectif) d'un microscope de telle sorte que l'image de A à travers L1, soit confondue avec F, foyer objet de la deuxième lentille ( oculaire ) du microscope. La distance focale de l'oculaire vaut f' = 3 cm. On écrit en bleu et gras les distances algébriques. Déterminer la grandeur A1B1 de AB donnée par la lentille L1. AO1 = 1,2 cm ; O1A1 = 14,4 cm. grandissement transversal : g =A1B1 / AB = O1A1 /O1A. A1B1 =AB* O1A1 /O1A = 1 10-5 *14,4 /(-1,2) = -1,2 10-4 cm. Sous quel angle visualise t-on A1B1 à travers l'oculaire ? a = 1,2 10-4 / 0,03 = 4 10-3 rad. L'utilisation du microscope permet-elle de séparer A et B ?  valeur supérieure au pouvoir séparateur de l'oeil : A et B sont distincts. 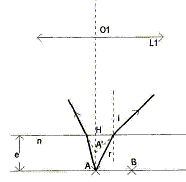Influence de la lame du microscope. On place sur l'objet à observer une lame de microscope d'épaisseur e = 2 mm et d'indice optique n =1,5. Déterminer la distance HA' sachant que les angles i et r sont petits. 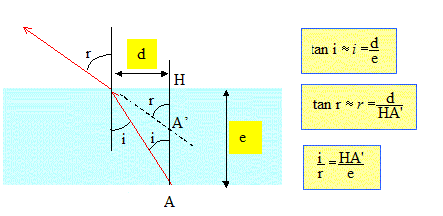Loi de Descartes pour la réfraction : n sin i = sin r : pour les angles petits : n i = r ( en radian) par suite HA' = e/n. Tout se passe comme si l'objet avait été rapproché d'une distance AA' = e(n-1)/n = 2*0,5/1,5 =0,667 mm du microscope. De quelle distance doit-on translater l'ensemble du microscope, pour obtenir un réglage identique au précédent ? L'image A1B1 doit se former au foyer objet F de l'oculaire.   L'objet étant plus proche, l'image A1B1 va se former à droite de F : il faut donc reculer le microscope de AA' =0,67 mm. .

retour -menu