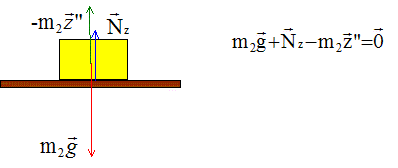Oscillation d'une masse posée sur un plateau concours Orthoptie Nantes 07

Un plateau de masse m1 est relié à deux ressorts verticaux identiques de constante de raideur k et de longueur à vide L0. L'origine O de l'axe z correspond à la position du plateau lorsque les deux ressorts ne sont ni tendus ni comprimés. Exprimer la valeur de zM à l'équilibre en foncfion de m1 et k. Elle sera notée z1. A l'équilibre du plateau, le poids de celui-ci neutralise la tension des ressorts. L1 : longueur du ressort à l'équilibre. m1g = 2 k(L0-L1) avec L0-L1= z1. z1= m1g/(2k). On abaisse le plateau de sa position d'équilibre d'une distance a (zM= z1-a) et on lâche le plateau sans vitesse initiale. 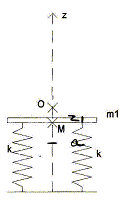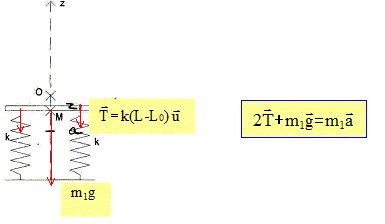Déterminer l'équation différentielle que doit satisfaire zM. Système : le plateau ; référentiel terrestre galiléen. Sur le schéma ci-dessous, le plateau est au dessus de la position d'équilibre :   Ecrire la deuxième loi de Newton suivant Oz : -2k(L-L0)-m1g = m1 z". Or L-L0 = L-L1+L1-L0 = z - z1. ( z : abscisse par rapport à la position d'équilibre) par suite -2k z + 2k z1-m1g = m1 z" d'où z" + 2k/m1 z. (1) z = zM +z1 : l'équation différentielle (1) est vérifiée par zM.      Montrer que l'équation horaire du mouvement du plateau s'écrit : zM=a1 cos (w1t+j)+b1. (1) est l'équation différentielle d'un oscillateur harmonique. La solution générale est du type : z = a1 cos (w1t+j) avec w1 = [2k/m1]½. z = zM +z1 ; zM = z-z1 ; zM = a1 cos (w1t+j) -z1.    Exprimer la pulsation w1 et la période T1 en fonction de k et m1. T1 = 2p/w1 ; T1 = 2p/ [m1/(2k)]½. A quoi correspond b1. A l'instant initial zM(t=0 ) = -z1-a ; zM(t=0 ) =a1 cos j +b1. On identifie : a = a1 cos j et b1 = -z1. Déterminer a1 et j à partir des conditions initiales. a = a1 cos j avec a1 amplitude positive d'où cos j =-1 soit j = p. zM = a cos (w1t+p) -z1.    Oscillations d'un objet de masse m2 posé sur le plateau. Exprimer la nouvelle valeur de zM à l'équilibre. Elle sera notée z2. A l'équilibre du plateau et de la charge, le poids total neutralise la tension des ressorts. L2 : longueur du ressort à l'équilibre. (m1+m2)g = 2 k(L0-L2) avec L0-L2= z2. z2= (m1+m2)g/(2k). On abaisse le plateau de sa position d'équilibre d'une distance a et on le lâche sans vitesse initiale. 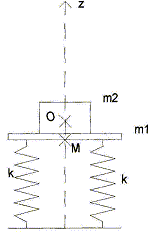Exprimer l'équation horaire du mouvement du plateau dans l'hypothèse d'un contact continu entre l'objet et le plateau. w2 : pulsation d'oscillation ; T2 : période d'oscillation. Même calcul que ci-dessus le système étant le plateau + la charge : on remplace m1 par m1+m2 et z1 par z2. zM = a cos (w2t+p) -z2.    Exprimer la pulsation w2 et la période T2.  w2 = [2k/(m1+m2)]½ ; T2 = 2p/w2 ; T2 = 2p/ [(m1+m2)/(2k)]½. Condition de décollage. Dans l'hypothèse d'un contact entre l'objet et le plateau, exprimer la réaction Nz(t) ( composante de la réaction suivant l'axe z) qu'exerce le plateau sur l'objet. Système : la charge de masse m2 ; référentiel non galiléen : le plateau Sur le schéma ci-dessous, le plateau se trouve au dessus de la position d'équilibre. Avant décollage, dans ce référentiel, la charge m2 est immobile : elle est soumise à son poids, à l'action du support et à une force d'inertie.   Projection sur l'axe Oz : -m2g +Nz + (-m2z")=0 ;  Nz = m2(g+z" ) Or z" = -w22 z ( dériver deux fois par rapport au temps z(t) ). Par suite : Nz =m2 (g -w22 z) avec z = a cos (w2t+p) Nz =m2g -am2w22 cos (w2t+p) = m2g +am2w22 cos (w2t) Montrer que cette réaction est la somme d'une constante et d'une fonction sinusoïdale à expliciter.  Nz =m2g -am2w22 cos (w2t+p). Montrer qu si a est supérieure à une valeur notér amin, l'objet posé sur le plateau décollera lors du mouvement. Dès que Nz s'annule, le solide de masse m2 décolle : m2g -aminim2w22 cos (w2t+p). aminiw22 cos (w2t+p) = g. Exprimer amini en fonction de g et w2.  La valeur maximale de cos (w2t+p) est 1 d'où amini = g/w22. Etude du cas : a >> amin. A quel instant t' ( exprimé en fonction de T2) et à quelle position l'objet décolle t-il du plateau ? w22 = g/amin ; Nz =m2g [ 1-a/amin cos (w2t+p)]. Au moment du décollage Nz=0 soit : 1=a/amin cos (w2t'+p)] amin /a = cos (w2t'+p) ; or a >> amini d'où 0 = cos (w2t'+p) cos (3p/2) = cos (w2t'+p) ; 3p/2 =w2t'+p t' = p / (2w2 ) ; avec w2 = 2p /T2 d'où t' =0,25T2. Le décollage a pratiquement lieu au passage à la position d'équilibre z2. Quelle est l'altitude h atteinte par l'objet h sera exprimé en fonction de a, k, g, m1 et m2) ? On considère le système { plateau + charge + ressorts } L'origine des énergies potentielles est prise à la position d'équilibre z2. L'énergie mécanique initiale du système est sous forme potentielle élastique : EM= 2*½ka2 = ka2 . Au passage à la position d'équilibre, l'énergie mécanique est sous forme cinétique : EM= ½(m1+m2)v2. La conservation de l'énergie mécanique conduit à : v2 = 2ka2/(m1+m2). Au point le plus haut, l'énergie mécanique de la charge m2 est sous forme potentielle de pesanteur : EM2= m2gh. L'énergie mécanique de cette charge, au moment du décollage était : EM2=½m2v2. Conservation de l'énergie mécanique : h = v2/(2g) ; h = ka2/((m1+m2)g). h est comptée à partir de la position d'équilibre z2. Par rapport à O, l'altitude atteinte est h-z2. Donner l'équation horaire du mouvement du plateau après décollage de l'objet. Le mouvement du plateau est un mouvement sinusoïdal de pulsation w1. L'abscisse initiale est -z2 ; la vitesse initiale est v = a[2k/(m1+m2]½. On choisit comme origine de l'axe vertical la position d'équilibre z1 et comme origine des dates, l'instant du décollage. z(t) = A sin( w1t+B) ; z(t=0) = z2-z1 d'où A sin B=z2-z1 ; l'amplitude A n'est pas nulle, donc B=arc sin((z2-z1 )/A). Déterminer notamment l'amplitude d'oscillation du plateau en fonction de a, z1, z2, m1 et m2. On choisit l'origine des énergies potentielles à la position d'équilibre z1. Energie mécanique du plateau au moment du décollage : EM1=½m1v2+k(z2-z1 )2. Au point le plus haut, l'énergie mécanique est sous forme potentielle élastique : EM1=kA2. La conservation de l'énergie mécanique conduit à : kA2 = ½m1v2+k(z2-z1 )2. A = [ m1/(2k)v2+(z2-z1 )2]½. Or v2 = 2ka2/(m1+m2). A = [ m1a2/(m1+m2)+(z2-z1 )2]½. Déterminer l'équation qui permet de déterminer le temps t'' au bout duquel l'objet retombe sur le plateau ( la résolution n'est pas demandée). Pour le plateau : z(t) = A sin( w1t+B). Pour la charge m2 : chute libre avec vitesse initiale v0 = a[2k/(m1+m2]½ , vers le haut, et position initiale z2-z1. On choisit comme origine de l'axe vertical la position d'équilibre z1 et comme origine des dates, l'instant du décollage. z" = -g ; z'=v = -gt+v0 ; z(t) = -½gt2 + v0t + (z2-z1). Lorsque la charge retombe sur le plateau : A sin( w1t"+B) = -½g t''2 + v0t "+ (z2-z1).

retour -menu