Propagation et détection d'un tsunami concours technicien météo 2008.

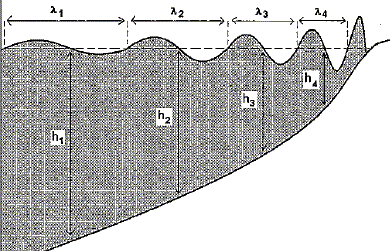
Partie 1 : propagation d'un tsunami. Untsunami est une vague géante ou une série de vagues, venant du fond de l'océan. Il peut être provoqué par un séisme : celui-ci provoque le soulèvement ou l'effondrement d'une partie du fond océanique, la masse d'eau situé au dessus est alors, sur plusieurs centaines de kilomètres brusquement déplacée. Un tsunami peut être assimilé à une onde circulaire se propageant depuis son point de formation, exactement comme les ronds dans l'eau qui apparaissent après avoir jeté un caillou dans une mare. La vitesse de propagation d'un tsunami est donnée par la relation v=(gh)½ avecg : intensité de la pesanteur et h la profondeur du fond océanique. En se rapprochant des côtes le tsunami perd de la vitesse, mais conserve presue la totalité de son énergie. Les vaques, en se rapprochant des côtes, prennent de l'amplitude. Lorsque le tsunami atteint le rivage, il peut prendre la forme d'une série de vaques déferlantes, au cours desquelles la mer monte et descend brusquement, ou d'un mur d'eau dévastateur. Le schéma ci-dessous représente qualitativement l'évolution de l'onde responsable d'un tsunami à l'approche des côtes. 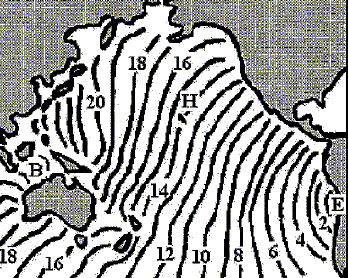On se propose d'étudier la propagation du tsunami qui, en 1960, fit plus de 2000 victimes au Chimi. Ce tsunami fut provoqué par un séisme dont l'épicentre E se trouvait au large des côtes chiliennes à une profondeur h0 = 7000 m. La carte ci-sdessous simule, heure par heure à partir de son déclenchement au niveau de l'épicentre E, la position du front de l'onde générée par ce séisme. Les valeurs de la vitesse de propagation v et la longueur d'onde l pour différentes profondeurs h sont données dans le tableau suivant. profondeur h (m) vitesse v ( km/h) longueur d'onde l( km) 7000 943 282 4000 713 213 2000 504 151 1000 ......... 107 200 159 48 50 79 23 10 36 10,6 Calculer la vitesse de propagation du tsunami à la profondeur h=1000 m. v=(gh)½ =(9,81*1000)½ = 99,0 m/s = 99,0*3,6 km/h =357 km/h. Rappeler la définition de la longueur d'onde. Quelle relation y a-t-il entre la longueur d'onde et la période de l'onde T ? La logueur d'onde l est la distance parcourue par le front d'onde, à la vitesse v, pendant une période T. l = v T. 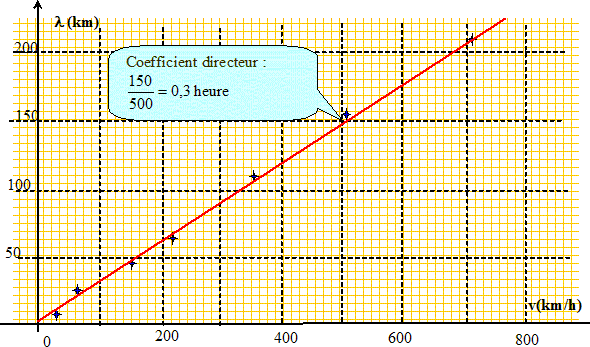Représenter la courbe l=f(v). Quelle est l'allure de cette courbe ? En déduire l'ordre de grandeur de la période T de l'onde. Doite dont le coefficient directeur est èagl à la période T ~ 0,3 h.   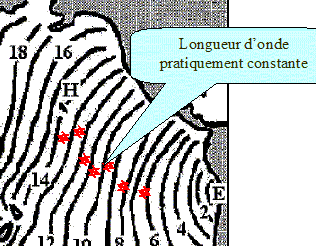On remarque que l'onde ne reste pas circulaire au cours de sa propagation. Justifier en quelques lignes l'évolution de la forme de l'onde au cours de sa propagation. La longueur d'onde est de l'ordre de quelques dizaines de kilomètres. Les obstacles, comme les côtes, sont du même ordre de grandeur que la longueur d'onde. En conséquence les côtes diffractent l'onde. Quel phénomène physique permet d'expliquer que le tsunami puisse atteindre la côte indonésienne ( point B) pourtant protégé par l'Australie ? Diffraction par les côtes ou par les bras de mer entre deux côtes. Après avoir parcouru la moitié du Pacifique, le tsunami frappe Hawaï ( point H) situé à environ 10 000 km de l'épicentre. Quelle est la durée de ce parcours ? lecture sur la carte ci-dessus : 14 heures. A quoi voit-on que la vitesse de propagation reste pratiquement constante sur cette distance ? Déterminer la vitesse moyenne de propagation dans cette partie du Pacifique. La distance parcourue par l'onde à chaque heure est pratiquement la même. vmoy = 10 000/14 ~ 710 km/h.   En déduire la profondeur moyenne du fond océanique. vmoy = 710 km/h = 710 / 3,6 =198 m/s v=(gh)½ ; h= v2 g = 1982 9,81 = 4000 m. L'onde produite à la date t=0 au niveau de l'épicentre peut être modélisée par une onde sinusoïdale. La position, par rapport au niveau moyen de l'océan, du point S situé à la surface de l'océan à la verticale de E est alors donné par : ( suivant un axe orienté vers le haut dont l'origine coïncide avec le niveau moyen) yS(t)= a sin 2 pt T Comparer le mouvement, par rapport au niveau moyen de l'océan, d'un point M situé à la distance dM =SM du point S à celui du point S. 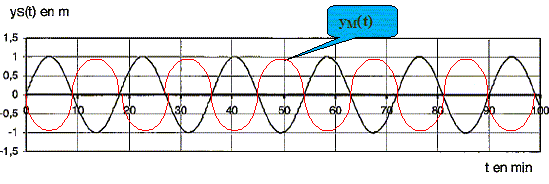En déduire l'expression de yM(t) en supposant que l'amplitude a reste inchangée et que la vitesse de propagation reste constante et égale à vmoy. Le mouvement du point M est identique à celui de la source S. Le point M reproduit le mouvement de la source avec un certain retard q= SM / vmoy= dM T /l. yM(t)= a sin 2 p(t- q) T = a sin 2 p[ t T - dM l ] La courbe yS(t) est représentée ci-dessous. Tracer sur cette figure l'allure de la courbe yM(t) pour dM=1, 5 l. Justifier. La distance SM est un multiple impair de la demi longueur d'onde : les points S et M vibrent en opposition de phase. 2pdM /l = 3p. 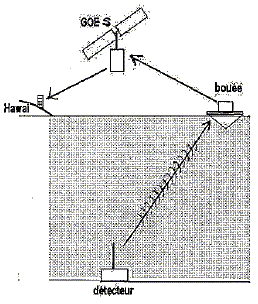yM(t)= a sin [ 2 p t T -3 p ] 2è partie : détection d'un tsunami. Afin d'améliorer la prévision des tsunamis en temps réel la NOAA a mis en place un réseau de détection . Il permet de détecter les mouvements en profondeur grâce à des capteurs de pression situés au fond de l'océan : le signal est envoyé par onde acoustique vers une bouée en surface qui envoie immédiatemment, sous forme d'onde électromagnétique, les informations au centre de contrôle d'Hawaï via un satellite géostationnaire. Rappeler la définition d'une onde transversale et d'une onde longitudinale. Onde transversale : la direction de déformation du milieu et la direction de propagation de l'onde sont perpendiculaires. Onde longitudinale : la direction de déformation du milieu et la direction de propagation de l'onde sont identiques. Quelle est la nature de l'onde acoustique ? Une onde acoustique est une onde mécanique progressive nécessitant l'existence d'un milieu de propagation. Quelle est la durée t nécessaire à la transmission d'une information entre le capteur de pression et la bouée en surface si la distance qui les sépare est d = 3000 m ? On donne la vitesse du son dans l'eau : veau = 1,5 103 m/s. t= d veau = 3000 1,5 103 = 2 s. Quelle est la durée t' nécessaire à la transmission d'une information entre la bouée et le satellite ? On donne : altitude d'un satellite géostationnaire H = 36 000 km ; c = 3,0 108 m/s. t'= H c = 3,6 107 3,0 108 = 0,12 s. En admettant que la durée de communication entre le satellite et le centre d'alerte soit égale à t', donner l'ordre de grandeur du temps séparant la détection du tsunami et le déclenchement de l'alerte. Conclure quant à l'efficacité de ce dispositif. environ 2 s ; ce dispositif est efficace : on dispose de plusieurs heures avant l'arrivée des vagues du tsunami pour mettre les populations à l'abri.

retour -menu