Chute parabolique concours technicien météo 2007.

Le lancer d'une balle est filmé avec un caméscope numérique. Le filme est ensuite visualisé image par image à l'aide d'un logiciel adapté qui permet de pointer la position du centre d'inertie G de la balle sur chaque image. On obtient ainsi les positions successives ( points Ai ) du centre d'inertie G à intervalles de temps réguliers t dans le plan du mouvement (Ox, Oy). L'axe Oy est orienté vers le haut, l'axe Ox est horizontal. 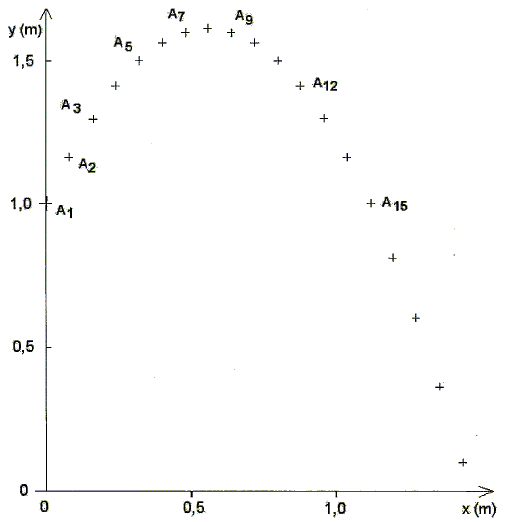Partie 1. Etude expérimentale.   Sachant que le film est pris à 20 images par seconde, déterminer t. t = 1 20 = 0,05 s Déterminer et tracer les vecteurs vitesses aux points A7 et A9.  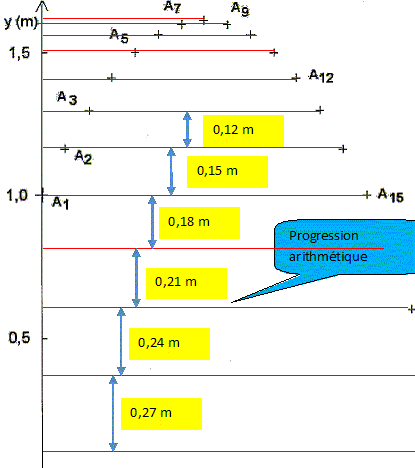Au point A7 : mesurer A6A7 et A7A8 au double décimètre. A6A7 = 8 mm ; A7A8 = 7 mm Tenir compte de l'échelle : 1 cm correspond à 0,1 m. A6A7 = 0,8 m ; A7A8 = 0,7 m v7 = A6A7 + A7A8 2t = 0,08+0,07 2*0,05 = 1,5 m s-1 Tracer la tangente à la trajectoire au point A7 ; choisir une échelle pour la vitesse : 1 cm correspond à 0,5 m/s. 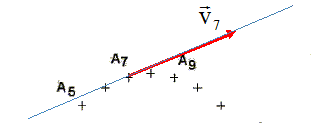Le vecteur vitesse a toujours le sens du mouvement.  Au point A8 : mesurer A9A8 et A10A9 au double décimètre. A9A8 = 7 mm ; A10A9 = 9 mm Tenir compte de l'échelle : 1 cm correspond à 0,1 m. 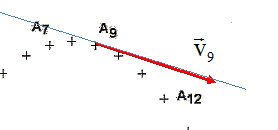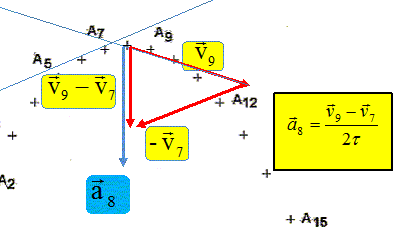A7A8 = 0,07 m ; A8A9 = 0,09 m v9 = A8A9 + A9A10 2t = 0,07+0,09 2*0,05 = 1,6 m s-1   Déterminer et tracer le vecteur accélération au point A8. 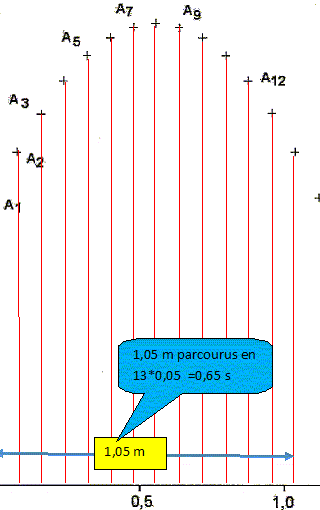Mesurer la longueur de la différence des deux vecteurs vitesses : ~ 2 cm Tenir compte de l'échelle des vitesses ( 1 cm <--> 0,5 m/s ) d'où 1 m/s. Diviser par 2 t d'où a8 = 1/0,1 = 10 m s-2. Ce vecteur est dirigé suivant la direction de l'axe Oy, mais en sens contraire de l'axe. Projeter les points Ai sur les axes Ox et Oy et en déduire la nature du mouvement de G suivant les axes Ox et Oy. Les droites "rouges" sont pratiquement équidistantes : le mouvement de G sur l'axe OX est uniforme. La valeur de la vitesse suivant l'axe OX, notée Vx est constante, égale à : Vx= 1,05/0,65 ~1,6 m/s. Suivant Oy, le mouvement est uniformément accéléré. 2è partie. Etude théorique. Masse de la balle m = 100 g ; intensité du champ de pesanteur g = 10 m s-2. Faire le bilan des forces appliquées à la balle dans le référentiel terrestre au cours de son mouvement. La bille n'est soumise qu'à son poids, verticale, vers le bas, valeur mg = 0,1 *10 = 1 N. En déduire les caractéristiques du vecteur accélération et comparer aux résultats précédents. La seconde loi de Newton conduit au vecteur accélération, verticale, vers le bas, valeur g = 10 m s-2. Composantes du vecteur accélération : ( 0 , -10 ). Résultats en accord avec ceux trouvés ci-dessus. Etablir les expressions littérales des équations horaires du mouvement du point G sur les axes Ox et Oy et comparer aux résultats précédents. Le vecteur vitesse est une primitive du vecteur accélération : Sur Ox : Vx = V0 x, composante horizontale de la vitesse initiale. Sur Oy : Vy = at +V0 y = -10 t + V0 y avec V0 y : composante verticale de la vitesse initiale. Le vecteur position est une primitive du vecteur vitesse : Sur Ox : x = V0 xt + x0 avec x0, abscisse initiale. On retrouve un mouvement rectiligne uniforme suivant Ox. Sur Oy : y = -5 t2 + V0 y t + y0, avec y0 ordonnée initiale. On retrouve un mouvement rectiligne uniformément accéléré suivant Oy.

retour -menu