Mécanisme de la foudre assimilé à la décharge d'un condensateur concours technicien météo 2007.

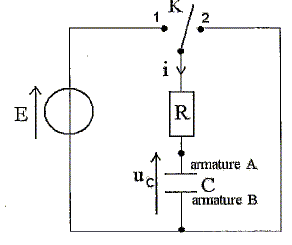
Partie 1. Etude de la charge et de la décharge d'un condensateur de capacité C. Le circuit électrique ci-dessous permet de réaliser la charge et la décharge d'un condensateur à travers un conducteur ohmique de résistance R. Sur quelle position doit être fermer le commutateur K pour réaliser la charge ? (1) : le condensateur est en série avec le générateur de tension. Sur quelle position doit être fermer le commutateur K pour réaliser la décharge ? (2) Montrer qu'en fin de décharge, le régime permanent étant atteint, la tension aux bornes du condensateur est égale à E. En régime permanent, l'intensité du courant est nulle ; la tension aux bornes du résistor R vaut alors UR= RI = R*0 = 0. Additivité des tensions : E = UC + UR = UC + 0 =UC. La charge étant terminée on bascule le commutateur K pour réaliser la décharge à la date t=0. Etablir l'équation différentielle vérifiée par la tension UC lors de la décharge.  Additivité des tensions : 0 = UC + UR avec UR = Ri ; qA= CUC. i = d qA dt = C d UC dt UC +RC d UC dt = 0 Vérifier que la fonction uC(t) = E exp (-lt) est solution de cette équation. En déduire l'expression de l en fonction des paramètres du circuit. Dériver UC(t) par rapport au temps : dUC/dt=-lEexp (-lt) Repport dans l'équation différentielle : E exp (-lt) + RC(-lE)exp (-lt)=0 Cette égalité est vérifiée quel que soit le temps t si : RC(-l) = -1 ; l= 1 RC Les courbes donnant l'allure des variations en fonction du temps de l'intensioté i(t) et de la tension UC(t) lors de la charge et de la décharge pour E= 4V, R= 1000 ohms et C= 5 microfarads sont données.  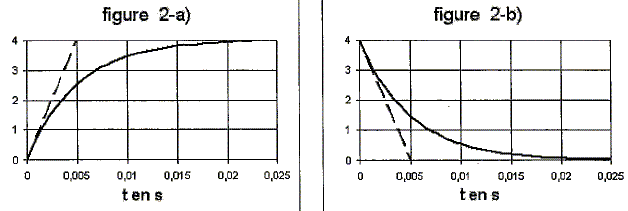Identifier ces courbes en justifiant. figure 2a : exponentielle croissante tendant vers une asymptote E= 4 V. Il s'agit de la tension aux bornes du condensateur en charge. figure 2b : exponentielle décroissante tendant vers zéro. La valeur initiale 4 V vérifie la continuité de la tension aux bornes du condensateur Il s'agit de la tension aux bornes du condensateur en décharge. 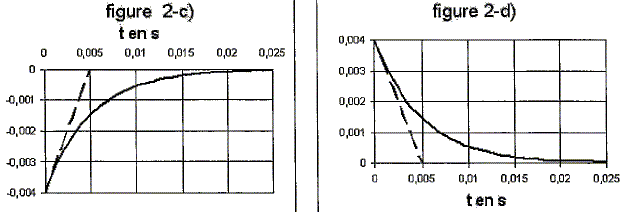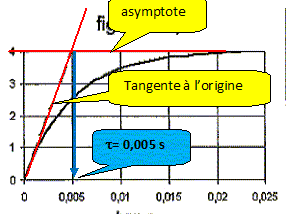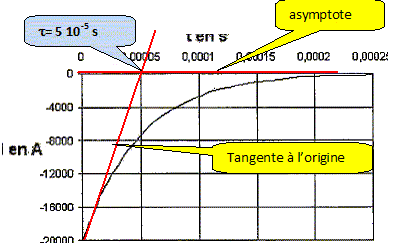figure 2d : exponentielle décroissante tendant vers zéro. La valeur initiale 4 mA correspond à E/R = 4/1000, intensité initiale Il s'agit de l'intensité du courant de charge. figure 2c : exponentielle croissante tendant vers zéro. La valeur initiale -4 mA correspond à -E/R = -4/1000, intensité initiale. On remarque la discontinuité de l'intensité et le changement de sens du courant de décharge par rapport à celui de charge. Il s'agit de l'intensité du courant de décharge. La tangente à l'origine tracée en pointillées pour chacune de ces courbes permet de déduire une grandeur notée t caractéristique du circuit. Quel nom donne t-on à t ? constante de temps. Déterminer graphiquement t. Donner l'expression de t en fonction des paramètres du circuit. Le calculer et comparer à la valeur trouvée ci-dessus. t= RC =1000*5 10-6 = 5 10-3 s Les deux valeurs sont en accord. Quelle relation existe t-il entre l et t ? l = 1 t   2è partie. Modélisation de la foudre. 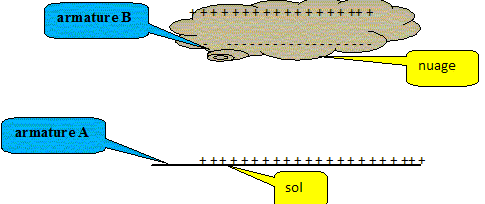Lors d'un orage, dans un nuage type cumulo-nimbus, de violents courants d'air ascendant entrainent des collisions entre particules d'eau et l'apparition de charges positives et négatives. Les charges de signes opposés se séparent : la base du nuage se charge négativement et la partie supérieure positivement. Simultanément le sol se charge positivement par influence. Il se forme ainsi un gigantesque condensateur de capacité C= 10 nF dont une armature est le sol ( armature A positive) et l'autre la base du nuage ( armature B négative) La tension entre ces armatures est alors E= 100 MV. Faire un schéma illustrant la situantion décrite ci-dessus. 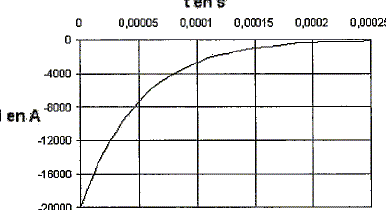La foudre correspond à la décharge de ce condensateur au travers de l'air, l'air étant assimilé à un conducteur ohmique de résistance R. On a relevé un pic de courant sur un conducteur métallique touché par la foudre. La courbe représentant les variations de l'intensité est donnée ci-dessous : L'intensité i(t) peut se mettre sous la forme i(t) = -i0 exp(-lt). Quelle est la valeur de i0 ? 20 000 A. Montrer que l'on a : i0 = E R A la date t=0, on exprime la tension aux bornes du condensateur de deux manière différentes : UC = E et UC= Ri0 avec R résistance électrique de l'air compris entre les armatures. En déduire la valeur de R quand la foudre se déclenche. E = 100 MV = 100 * 106 V = 108 V. R= E i0 = 108 20 000 = 5000 ohms. Déterminer graphiquement la valeur de t ; en déduire R et conclure. R= t C = 5 10-5 10 10-9 = 5000 ohms. Les deux valeurs trouvées pour R sont identiques. 3è partie. Propagation de l'onde sonore. La foudre s'accompagne d'une onde sonore : le tonnerre. Cette onde est engendrée par la brutale dilatation de l'air surchauffé ( la température peut atteindre 30 000 °C). Comparer la vitesse de propagation du son dans l'air et la vitesse de propagation de la lumière dans l'air. Conclure.. vson ~ 300 m/s ; vlumière = 3 108 m/s. Un observateur placé à quelque distance perçoit d'abord l'éclair et seulement ensuite le bruit du tonnerre. Déterminer le temps qui s'écoule entre la vision de l'éclair et la perception du bruit du tonnerre si l'observateur se trouve à 3 km du lieu où éclate la foudre. La lumière parcourt 3 km en une durée négligeable par rapport au son. t = 3000/300 = 10 s.

retour -menu