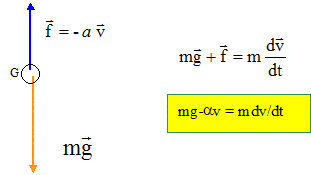Mécanique : chute dans un liquide ; électricité : triphasé ingénieur territorial interne 2008.

Les vecteurs sont écrits en gras et en bleu. Un garçon laisse tomber dans un puits, sans vitesse initiale, un caillou de forme sphérique et de masse m. La surface de l'eau se situe à une distance h du point de lâché du caillou. Dans l'air le caillou n'est soumis qu' à son poids, les frottements de l'air étant négligés. Dans l'eau il est soumis en plus à une force de frottement f proportionnelle à la vitesse v : f = -av. La poussée d'Archimède est négligeable dans les deux milieux. Démontrer que quelle que soit sa vitesse d'impact, le caillou atteint dans l'eau une vitesse constante que l'on calculera. m =200 g ; a= 0,2 kg s-1 ; g = 9,81 m/s2. Référentiel terrestre supposé galiléen : axe vertical orienté vers le bas ; origine : altiude h au dessus de la surface libre de l'eau. Dans l'air, le caillou n'est soumis qu'à son poids : chute libre sans vitesse initiale. v =gt et z = ½gt2. ; t = v/g soit z = ½g (v/g)2 = ½v2/g. vitesse d'arrivée à la surface de l'eau : v0 = [2gh]½. Dans l'eau :     Equation différentielle de la vitesse : dv/dt + a/m v = g (1). Solution générale de dv/dt + a/m v =0 : v = A exp(- at/m), avec A une constante. Solution particulière de (1), la vitesse limite : a/m v lim= g ; v lim= mg/a. Solution générale de (1) : v = A exp(- at/m) + mg/a. On choisit l'origine des temps au moment de l'impact sur l'eau. A l'instant initial, la vitesse est v0 = [2gh]½. v0 = A+mg/a ; A = v0 -mg/a. v = v0 exp(- at/m) + mg/a ( 1-exp(- at/m)). Lorsque t devient grand, exp(- at/m) tend vers zéro : la vitesse tend ver une vitesse limite : v lim= mg/a. v lim= mg/a = 0,2*9,81/0,2 ; v lim= 9,81 m/s. Quelle doit être la distance h, pour que ce caillou, après la chute libre dans l'air, possède dans l'eau un mouvement rectiligne uniforme ?  D'après le principe d'inertie, si le mouvement est rectiligne uniforme, alors , dans l'eau les forces se compensent.  av = mg ; la vitesse d'impact sur l'eau doit être égale à la vitesse limite v lim= mg/a. de plus cette vitesse est égale à v0 = [2gh]½ = 9,81 m/s. 2gh = 9,812 = 96,2 ; h = 96,2/ 19,62 ; h = 4,9 m.     Electricité. Une installation électrique triphasée est équivalente à trois impédances identiques de résistance R= 12 W et de réactance inductive 9 W branchée en triangle sur le secteur 230/400 V - 50 Hz. Calculer la puissance active, réactive et apparente de cette installation. Impédance Z = (R2+X2)½ = (144+81)½ ; Z = 15 W. Le facteur de puissance est cos j = R/Z = 12/15 ; cos j = 0,8 ; sin j = 0,6. Dans un montage triangle, la tension aux bornes d'une impédance est la tension composée U = 400 V. Intensité efficace traversant une impédance J = U/Z = 400/15 = 26,67 A. Intensité efficace en ligne : I = J*3½ = 26,67*1,732 ; I = 46,2 A. Puissance active P = 3½U I cos j =1,732*400*46,2*0,8 ; P = 25600 W. Puissance réactive : Q = 3½U I sin j =1,732*400*46,2*0,6 ; Q = 19200 var. Puissance apparente S == 3½U I = P /cos j = 25600/0,8 ; S = 32000 V A. En réalité cette installation triphasée est constituée : - d'un four de séchage comprenant 3 résistances identiques R montées en étoile - d'un appareil équivalent à 3 inductances pures identiques L branchées aussi en étoile. Calculer R et L.  Dans un montage étoile, la tension aux bornes du dipole est la tension simple V=230 volts et l'intensité en ligne I est l'intensité qui traverse le dipôle. Seules les résistances consomment de la puissance active ; le facteur de puissance vaut 1. d'où : 25600 = 3½UI avec V=RI soit I = V/R ; 25600 = 3½U V/R = U2/R. R = 4002 /25600 ; R=6,25 W. Le inductances pures consomment de la puissance réactive et sin j = 1. d'où : 19200 = 3½UI avec V=X I soit I = V/X ; 19200 = 3½U V/X = U2/X. X = 4002 /19200 ; X=8,33 W. X = Lw avec w = 2pf = 314 rad/s. L = X/w =8,33 / 314 ; L = 2,65 10-2 H.

aite

retour -menu