Trombone de König, fusion deutérium tritium concours ingénieur Geipi ENI 2008

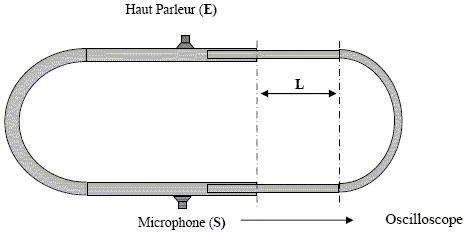
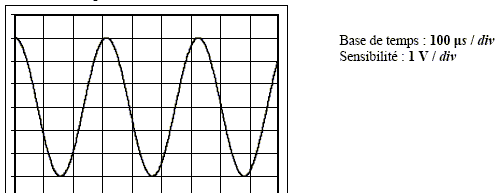
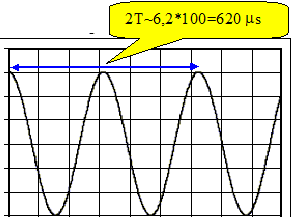
Le “trombone” de König (physicien allemand du 19ème siècle) est un dispositif permettant de mesurer des longueurs d’ondes acoustiques. On se propose d’utiliser ce dispositif afin de déterminer la célérité d’ondes acoustiques dans l’argon. Un haut-parleur émet l’onde à l’entrée E. Un microphone placé à la sortie S permet de recueillir le signal après que l’onde s’est propagée dans les deux branches du “trombone”. On appellera d1 la distance parcourue dans la branche fixe (partie gauche), et d2 la distance, réglable, parcourue par l’onde dans la branche mobile (partie droite). Lorsque la partie mobile est glissée au maximum dans la partie fixe (L = 0), les distances sont égales dans les deux branches. On réalise l’enregistrement suivant :   Déterminer la période et la fréquence des ondes acoustiques utilisées. T = 310 ms = 3,1 10-4 s ; f = 1/T = 1/3,1 10-4= 3,2 103 Hz. De quel type d’ondes s’agit-il ? Onde mécanique longitudinale progreesive périodique. ( son aigu ) A quelle condition sur L l’onde arrivant par la branche droite est-elle en phase avec l’onde arrivant par la branche gauche ? d2-d1 =2L doit être un multiple de la longueur d'onde l. L = ½k l. On admet que les signaux observés correspondent à la somme des ondes qui se sont propagées dans les deux branches. Qu’observe-t-on si les deux ondes arrivent en opposition de phase en S ? La supperposition est destructive : on observe un trait horizontal au centre de l'écran. Qu’observe-t-on si les deux ondes arrivent en S en phase ? La supperposition est constructive : onde sinusoïdale de fréquence 3200 Hz et d'amplitude double soit 6 V. On fait maintenant varier la longueur L ; on observe qu’il faut faire varier L de 5,4 cm entre deux positions où les ondes sont en phase. Déterminer la longueur d’onde des ondes utilisées. l = 2L = 10,8 cm. En déduire la célérité des ondes utilisées dans cette étude. c= l f = 0,108*3200 = 3,46 102 m/s.   Fusion deutérium tritium. On étudie la formation d'hélium à partir de deutérium et de tritium ; cette réaction nucléaire libère un neutron. Equilibrer la réaction : 21H + 31H--> AZHe +10n + g. Conservation de la charge : 1+1 =0+Z ; Z=2. Conservation du nombre de nucléons : 2+3 = A+ 1 : A =4. 21H + 31H--> 42He +10n + g. Comment appelle-t-on ce type de réaction nucléaire ? fusion nucléaire. Comment peut-on qualifier les trois nucléides : deutérium, tritium et hydrogène ? Même nombre de charge Z et des nombres de neutrons différents : isotopes. particule deutérium tritium helium neutron masse (u) 2,01355 3,01550 4,00150 1,00866 e= 2,998 108 m/s ; 1 u = 1,66054 10-27 kg ; NA =6,023 1023 mol-1 ; h=6,626 10-34J s. Montrer que le système (hélium + neutron) est plus stable que le système (deutérium + tritium). Il suffit de montrer que Dm est négatif. Dm = m(42He ) + m(10n ) - m(21H)-m(31H) Dm =4,00150+1,00866-3,01550-2,01355 =-0,01889 u. Calculer l'énergie El libérée par cette réaction. El = |Dm |c2 avec |Dm |= 0,01889*1,66054 10-27 =3,13676 10-29 kg El = 3,13676 10-29*(2,998 108)2=2,81932 10-12 J ~2,819 10-12 J. Calculer l'énergie el libérée par kg de matière utilisée. m(21H)+m(31H) = 8,351 10-27 kg el = 2,81932 10-12 / 8,351 10-27 = 3,376 1014 J kg-1. Que représente g ? photons encore plus énergétiques que les RX. En supposant que g véhicule toute l'énergie libérée par la réaction, déterminer la fréquence et la longueur d'onde associées. El = h f ; f = El / h =2,81932 10-12 / 6,626 10-34 = 4,255 1021 Hz. l = c/f ; l = 2,998 108 / 4,255 1021 =7,046 10-14 m.

retour -menu