Charge et décharge d'un condensateur ; fentes d'Young ; interférences concours contröleur répression des fraudes 2006

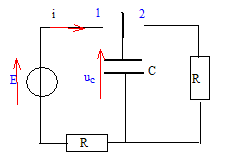
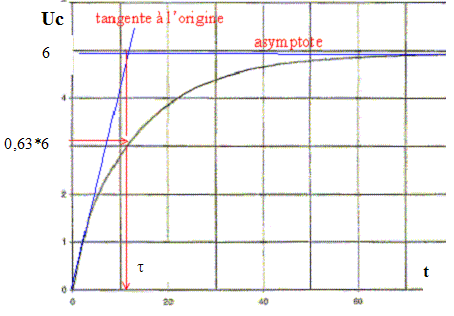
Charge et décharge d'un condensateur. Le circuit ci-dessous comporte : - un générateur de tension de force électromotrice E = 6,0 V, un conducteur ohmique de résistance R = 4,70 kW, - un condensateur de capacité C = 22,0 µF. Le commutateur à deux directions K permet, dans la position 1, de relier le dipôle RC au générateur et, dans la position 2 de court-circuiter le dipôle RC.  On place K dans la position 1 à la date t = 0 s. Écrire la loi des mailles en respectant le sens des flèches indiquées sur le schéma. E = uC+Ri Écrire la relation qui lie l'intensité i du courant à la charge électrique q traversant une portion de circuit. i = dq/dt Écrire la relation qui lie la tension uC aux bornes du condensateur et sa charge électrique q. q=CuC. Déduire des trois questions précédentes l'équation différentielle traduisant les variation de la tension uC aux bornes du condensateur en fonction du temps. i = CduC/dt ;  E = uC+ RCduC/dt ; duC/dt + 1/t uC = E/t. (1) avec t = RC. Vérifier que la fonction uC =E(1-exp(-t/(RC)) est solution de cette équation différentielle en supposant le condensateur non chargé à la date t = 0 s. duC/dt = E/t exp(-t/t). Repport dans (1) : E/t exp(-t/t) + E/t(1-exp(-t/t) = E/t. E/t exp(-t/t) + E/t - E/t exp(-t/t) = E/t égalité vérifiée quel que soit le temps. Calculer la constante de temps t du circuit. t = RC = 4,7 103 * 22 10-6 = 0,10 s. Construire sommairement la courbe représentant les variations de uC en fonction du temps après avoir tracé l'asymptote et la droite tangente à l'origine de cette courbe. Établir l'expression de la relation i(t) traduisant les variations de l'intensité du courant qui traverse le circuit au cours de l'expérience. q(t) = CUc(t) = CE(1-exp(-t/t)) i(t) =dq(t)/dt = CE/t exp(-t/t)) ; i(t) = E/R exp(-t/t)). Quelle est, au cours de la charge, l'expression de l'énergie du condensateur en fonction du temps ? EC =½CUc2(t) = ½CE2 [1-exp(-t/t)]2. En appelant ECm l'énergie du condensateur à la fin de la charge, calculer le rapport EC/ECm à la date t = t. ECm =½CE2 ; EC (t)=½CUc2(t) = ½CE2 [1-exp(-1)]2= ½CE2*0,632 = ½CE2*0,4. EC/ECm =  0,4.   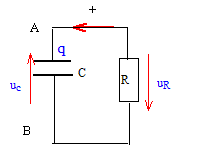Le commutateur K est maintenant basculé dans la position 2. Cet instant est choisi comme nouvelle origine des temps t = 0 s. Écrire la loi des mailles en respectant le sens des flèches indiquées sur le schéma. À l'instant t = 0, le condensateur est chargé sous la tension uC(0) = E = 6 V. L' intensité a été comptée positivement au cours de la charge du condensateur. La flèche surmontée d'un signe + indique le sens positif de parcours du circuit En déduire l'équation différentielle à laquelle obéit la tension uC au cours de cette phase de l'expérience. La loi d'additivité des tensions donne la relation entre uR et uC : uR + uC =0 ; Ri + uC =0 (1) La charge q de l'armature du condensateur est liée à la tension uC : q = C uC La relation liant l'intensité i du courant à la tension uC s'écrit : i = dq/dt ou encore i = q', dérivée de la charge par rapport au temps. or q = C uC d'où q' = C duC/dt soit q' = Cu'C. par suite i = Cu'C et Ri = RC u'C repport dans (1) : RC u'C + uC =0 L'équation différentielle régissant l'évolution de uC s'écrit : u'C + 1/(RC) uC =0. On note RC= t d'où : u'C + 1/t uC =0.(2) Vérifier que la fonction uC =E exp(-t/(RC)) est solution de cette équation différentielle en supposant que K avait été fermé suffisamment longtemps dans la position 1 pour que la charge du condensateur soit terminée. duc/dt = -E/t exp(-t/t)) ; repport dans (2) : -E/t exp(-t/t)) + 1/t E exp(-t/t)) = 0, égalitée vérifiée quel que soit le temps. Établir la relation traduisant les variations de l'intensité du courant i(t) au cours de la décharge. i(t) = Cduc/dt =   -CE/t exp(-t/t)) = -E/Rexp(-t/t)).   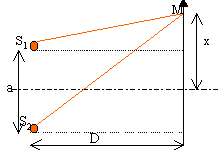Fentes d'Young  Une fente source F éclaire deux fentes fines F1 et F2 identiques et parallèles entre-elles. Les fentes F1 et F2 sont distantes d'une distance a. Soit un point M d'abscisse x sur un écran (E), de centre O, parallèle au plan des fentes F1F2. On appelle D la distance entre le plan des fentes et l'écran : D = 1,0 m. La fente F est dans le plan médiateur de F1F2 et est éclairée par une lampe à vapeur de sodium qui émet une lumière monochromatique de longueur d'onde l = 589 nm.   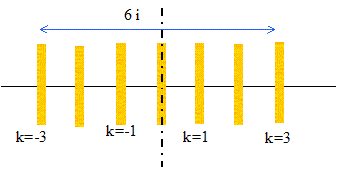Pourquoi doit-on faire un montage aussi compliqué pour obtenir une figure d'interférences ? Ne serait-il pas plus simple d'éclairer l'écran avec deux lampes identiques ? Les interférences ne peuvent avoir lieu qu'entre deux ondes cohérentes. Dans la région où se superposent les ondes, l'intensité lumineuse passe par des maximums et des minimums qui peuvent être nuls. Les maximums dépassent la somme des intensités des faisceaux pris séparément. A partir d'une source ponctuelle et monochromatique, il suffit de diviser l'onde en deux sources secondaires. Ces 2 sources secondaires issues d'une même source sont cohérentes. Établir l'expression de la différence de marche d au point M en fonction de x, D et a. Faire un schéma pour appuyer votre démonstration.   différence de marche d = n (S1M-S2M) . Tout le système est plongé dans le même milieu d'indice n. On supposera D >> a soit S1M + S2M voisin 2 D. S1M²=D²+(x-0,5 a)² S2M²=D²+(x+0,5 a)² S2M² -S1M² = (x+0,5 a)²-(x-0,5 a)² (S2M-S1M)(S1M+S2M) = 2 a x S2M-S1M voisin a x /D d = n a x /D ; dans l'air n=1. Citer la définition de l'interfrange. Déduire de la question précédente et de la définition, l'expression de l'interfrange i. interfrange (i): distance séparant les milieux de deux franges consécutives de même nature. Interférences constructives ( maximum de lumière) si la différence de marche est un multiple entier de la longueur d'onde l. d = a x /D = kl ; k=1 donne x1 = l D / a ; k=2 donne x2 = 2l D / a ; i = x2-x1 = l D / a. La distance séparant les deux franges brillantes d'ordres +3 et -3, mesurée en utilisant un oculaire micrométrique vaut 5,9 mm. En déduire, à l'aide d'un schéma, la valeur de l'interfrange i puis calculer la distance a entre les fentes F1 et F2.   i = 5,9 10-3 / 6 = 9,83 10-4 m. a = l D / i = 589 10-9 *1,0 / 9,83 10-4 = 5,8=5,98 10-4= 6,0 10-4 m.

retour -menu