Concours ergothérapeute Créteil et Adere 2008 dipôle LC ; mouvement rectiligne uniformément accéléré

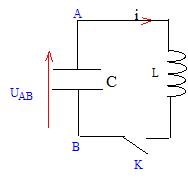
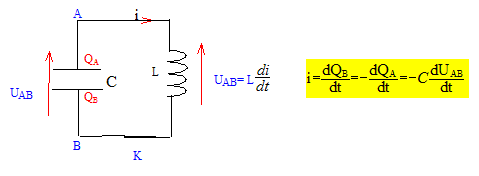
Dans ce montage l'interrupteur K est ouvert, la bobine d'inductance L a une résistance négligeable. Le condensateur de capacité C est préalablement chargé, la tension à ses bornes est : U0=10V. A l'instant t=0 on ferme K. Aide aux calculs : (2)½=1.4, pi~3.14 Nommer le phénomène obtenu et écrire la relation entre i(t); C et dUc/dt. Echange permanent d'énergie entre condensateur et bobine. Ce dipôle LC constitue un oscillateur électrique libre non amorti.     Etablir avec rigueur l'equation différentielle en Uc régissant le phénomène. UAB = Ldi /dt avec di/dt = -Cd2UAB/dt2. UAB =-LCd2UAB/dt2 ; d2UAB/dt2 + 1/(LC) UAB =0 ; on pose 1/(LC) = w2.   Des enregistrements à l'aide d'une carte d'acquisitions ont permis de déterminer les expressions de Uc(t) et i(t) Uc = 10.cos(104t) (V) et i(t) =10.10-3.sin(104t) (A) Montrer, à l'aide de la relation établie à la première question, que C=100nF. i= -C dUAB/dt = -C *10(-104) sin (104t) = 105 C sin (104t) On identifie 105 C à 10.10-3 d'où C = 10-7 F = 100 10-9 F = 100 nF. Calculer la valeur de l'inductance en mH.   1/(LC) = w2 avec w = 104 rad/s. L = 1/(Cw2 ) = 1/(10-7*108) = 0,1 H. Donner expression période propre du circuit puis sa valeur numérique en ms. T = 2p(LC)½ = 6,28 (0,1*10-7)½ = 6,28 10-4 s = 0,628 ms~ 0,63 ms. Donner l'expression littérale de l'énergie mise en jeu puis donner sa valeur numérique en microjoules. E= ½CU02 = 0,5 *10-7 * 100 = 5 10-6 J = 5 mJ. Soit t1 la date à laquelle la pour la première fois après fermeture de K 50% de l'énergie se trouve dans le bobine et 50% dans le condensateur. Déterminer les expressions littérale de U(t1) et i(t1), puis leurs valeurs numériques. ½CU2(t1)=  0,5 ( ½CU20 ) ; U2(t1) / U20 = 0,5 ; U(t1) / U0 =0,5½ = 0,707. U(t1) / U0 = cos(104t1)   = 0,707 = cos (p/4) d'où 104t1 = p/4 U(t1) = 10 cos (p/4) = 70,7 V ~ 7,1 V. i(t1) = 0,01 sin (104t1) = 0,01 sin(p/4) =0,01*0,707 = 7,1 10-3 A.      Un mobile M se déplace le long d'un axe Ox avec une accélération constante a. Etablir l'équation horaire de son mouvement. La vitesse est une primitive de l'accélération v(t) = at + v0 avev v0 vitesse à la date t=0. L'abscisse x(t) est une primitive de la vitesse : x(t) = ½at2 + v0t + x0 avec x0 abscisse à la date t=0. Sachant que le mobile part de l'origine O à l'instant t = 0 et sans vitesse initiale, que devient l'équation horaire de son mouvement ? x(t) = ½at2 A partir d'un instant t0 fixé, on mesure les segements de droite parcourus par le mobile M pendant des intervalles de temps successifs de même durée q. Donner l'expression de x0, abscisse du mobile M à l'instant t0. x0 = ½at20. Déterminer les expressions de x1, x2, x3, abscisses du mobile M aux instant respectifs t0+ q, t0+2q et t0+ 3q. x1 = ½a(t0+q)2 ; x2 = ½a(t0+2q)2 ; x3 = ½a(t0+3q)2 . En déduire les expressions des segments parcourus successifs : x1-x0, x2-x1 et x3-x2. x1-x0= ½a[ (t0+q)2 -t20 ]= ½aq2 + aq t0. x2-x1 =½a[ (t0+2q)2 - (t0+q)2]= 1,5aq2 + aq t0 . x3-x2 =½a[ (t0+3q)2 - (t0+2q)2]= 2,5aq2 + aq t0. Montrer que ces segments forment une progression arithmétique dont on déterminera la raison r. x2-x1 =  x1-x0 + aq2 ; x3-x2 =x2-x1 + aq2. Application : le mobile M est une rame de métro qui, à partir de l'instant t0, parcourt 24 m pendant les 2 premières secondes puis 32m pendant les 2 secondes suivantes. Calculer la valeur a de son accélération. q = 2 s ; x1-x0= 24 ; x2-x1 =32 d'où 32 = 24 + a*4 ; a = 2 m s-2.

retour -menu