Gravitation, Kepler, rotation d'une quille de voilier concours EPF 2007

Gravitation, Kepler. En juillet 2006, la sonde européenne Cassini-Huygens a photographié Titan nous livrant de précieuses informations sur la constitution de ce satellite de Saturne. Ainsi, l’atmosphére de ce satellite serait similaire à celle de la Terre à son origine. On admet que les trajectoires des satellites autour de Saturne sont circulaires. Données : G = 6, 67 × 10-11 S.I ; Titan : RT = 1, 22 × 106 km (rayon autour de l’orbite de Titan). Concernant Saturne : RS = 6, 0 × 104 km (rayon de la planète Saturne). TS = 10h 39 min (période de rotation de Saturne sur elle-même). MS = 5, 69 × 1026 kg (masse de Saturne). • Concernant Encelade : TE = 1, 37 jours terrestres (période de révolution). On considèrera que Saturne et Titan ont des répartitions de masse à symétrie sphérique. Ainsi, on résumera Saturne et Titan à leur centre de gravité respectif S et T. Les vecteurs sont écrits en gras et en bleu. Soit u le vecteur unitaire porté par la droite ST et dirigé de S vers T. Enoncer la loi de gravitation en l’appliquant au système (Saturne-Titan). Donner l’expression vectorielle de la force exercée par Saturne sur Titan et la représenter sur un schéma. Deux corps A et B de masses respectives mA et mB séparés d'une distance d exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit. Ces forces sont proportionnelles aux masses et inversement proportionnelles au carré de la distance d.     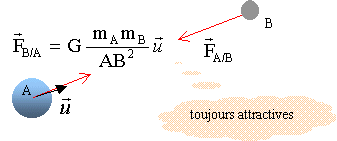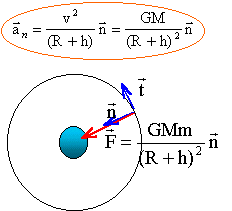Etablir l’expression vectorielle de l’accélération a de Titan dans le référentiel de Saturne que l’on considèrera galiléen. Le satellite est soumis à la seule force de gravitation centripète exercée par la planète M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol Montrer que le mouvement circulaire de Titan est uniforme. La force de gravitation est toujours perpendiculaire à la vitesse ; cette force ne travaillant pas, elle ne modifie pas la valeur de la vitesse : le mouvement est donc uniforme. Etablir l’expression de la vitesse de Titan sur son orbite autour de Saturne et la calculer. suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m aN= mv²/ (R+h) d'où la valeur de la vitesse (m/s): v² =GMS / (RS+h) =GMS / RT. indépendante de la masse du satellite     v = [GMS / RT]½ = [6, 67 × 10-11*5, 69 × 1026 / 1, 22 × 109 ]½ =5,58 103 m/s ( 5,5775 103)   La 3eme loi de Kepler n’est pas la loi des aires mais celle des périodes. On supposera qu’Encelade a un mouvement circulaire uniforme. Donner l’expression de la vitesse vE d’Encelade en fonction de sa période TE et du rayon RE de sa trajectoire. Encelade décrit une circonférence de rayon RE à la vitesse vE durant une période TE . vE =2pRE /TE . Montrer que l’on peut retrouver la 3eme loi de Kepler. D'une part : vE2 =GMS / RE ; d'autre part : vE2 =4p2R2E /T2E . d'où : T2E = 4p2 /(GMS ) R3E. Calculer la valeur du rayon RE de l’orbite d’Encelade. RE = [T2EGMS / (4p2)]1/3 avec TE = 1, 37 jours terrestres = 1,37*24*3600 s = 1,1837 105 s. RE = [ 1,18372 1010 *6, 67 × 10-11*5, 69 × 1026 / (4*3,142)]1/3 =2,38 108 m. Cassini, un satellite stationnaire à orbite circulaire. Qu’est-ce qu’un satellite géostationnaire ? Quelle condition doit-on avoir sur les périodes TS (rotation de Saturne sur elle-même) et TC (révolution de Cassini autour de Saturne) pour que la sonde soit ”Saturno-stationnaire” ? On propose deux trajectoires hypothéthiques d’un satellite en mouvement circulaire uniforme autour de Saturne : Montrer que seule l’une des trajectoires est réaliste. En effet un satellite géostationnaire est un satellite qui a une position fixe par rapport au référentiel lié à Saturne ( il reste en permanence à la verticale d’un même point du sol) Pour être géostationnaire le satellite doit avoir: * une trajectoire circulaire de centre O, centre de Saturne * pour période de révolution celle de Saturne : TS =TC. *et de plus il doit tourner dans le même sens que Saturne avec le même axe de rotation : donc le plan de sa trajectoire est perpendiculaire à l’axe de rotation de Saturne et il contient le point O : le plan de la trajectoire est obligatoirement équatorial. La trajectoire 1 convient. Déterminer l’altitude h de la sonde. Calculer la valeur de h. Ecrire la 3ème loi de Kepler : T2S = 4p2 /(GMS ) R3C. RC = [T2SGMS / (4p2)]1/3 avec TS = 10h 39 min = 36000 +39*60 s = 3,834 104 s. RC = [ 3,8342 108 *6, 67 × 10-11*5, 69 × 1026 / (4*3,142)]1/3 =1,12 108 m. RC=RS+h soit h = RC-RS= 1,12 108-6, 0 × 107 = 5,2 107 m.   rotation d'une quille de voilier. Un voilier monocoque 60 pieds, destiné à la course Vendée Globe, possède une quille en acier constiuée d’un voile de quille et d’un bulbe (lest), voir schéma ci-contre. Le skipper peut incliner la quille par rapport à la coque du bateau et la maintenir avec un angle fixe lors de la navigation pour augmenter les performances du voilier. Lors d’un examen du voilier on souhaite vérifier les propriétés oscillatoires de la quille. La masse du voile de quille est négligeable devant celle du lest. La quille peut donc être assimiléee à un pendule simple de longueur L= 3, 5 m et de masse M = 4, 0 tonnes. Les oscillations seront supposées non amorties. On notera g l’intensité de la pesanteur. On donne g = 9, 81 m/s2. 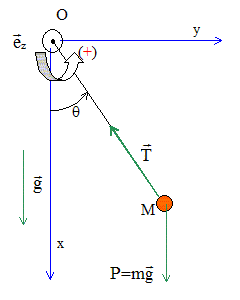A l'instant de date t = 0 s, la quille est écartée de sa position d'équilibre d'un angle a = 30° et abandonnée sans vitesse initiale. Montrer que la période pourrait être propotionnelle (L/g)½ à l'aide d'une analyse dimensionnelle. L a la dimension d'une longueur [L] = L g a la dimension d'une accélération, soit une longueur divisée par un temps au carré: [g]=L T-2. [L/g]= T2 et [(L/g)½] = T. A l'instant de date t, le centre de gravité de la quille fait un angle q avec la verticale. Repésenter sur un schéma les forces s'exerçant sur le lest. Déterminer la valeur de la force T exercée par le voile de quille sur le lest en fonction de L, M, q, g et de v(t), valeur de la vitesse du centre d'inertie du lest à la date t. Ecrire la seconde loi de Newton sur l'axe OM, orienté vers O : T -mg cos q = maN = mv2/L. T = m[v2/L+ g cos q]. Exprimer en fonction de L, M, q et g le travail des forces sur le lest. T est perpendiculaire à chaque instant à la vitesse : cette force ne travaille pas. Travail moteur du poids de t=0 à la date t : mg L ( cos q-cos a). Déterminer la vitesse v(t) du lest à l'instant de date t. Ecrire le théorème de l'énergie cinétique entre l'instant t=0 et la date t : ½mv2-0 = mgL( cosq-cosa) v = [2gL( cosq-cosa)]½.   Donner l'expression de la valeur de la force T en fonction de m, g et q. Calculer T au moment du lancer ( q = 30°) puis au moment où le centre d�finertie du lest passe par la verticale ( q = 0° ). T = m[v2/L+ g cos q] et v2/L =2g( cosq-cosa) d'où : T = mg (3cosq-2cosa). T30 =4000*9,81( 3cos30-2 cos30) = 3,4 104 N. T0 =4000*9,81( 3cos0-2 cos30) = 5,0 104 N. Déterminer l'expression de l'énergie cinétique du lest ainsi que l'action du lest sur le voile de quille lors de son passage à la verticale. Ec = ½mv2 = mgL( cosq-cosa) Ec 0° = mgL( 1-cosa). Principe des actions réciproques : l'action du lest sur le voile est opposé à l'action du voile sur le lest.

retour -menu