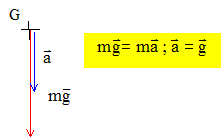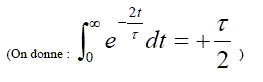Principe du sonar, chute libre, microgravité, dipôle RC EMIA 07

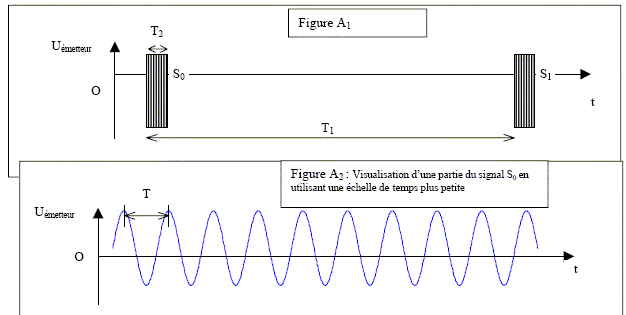
Le sonar est un dispositif émetteur/récepteur d’ondes ultrasonores qui, remorqué par un navire, permet d’obtenir des enregistrements donnant une image à deux dimensions des fonds marins ou encore de détecter des submersibles.

Les rayons ultrasonores qui matérialisent la direction et le sens de propagation de l’onde ultrasonore sont très peu inclinés par rapport à la verticale. On considérera donc que le trajet accompli par l’onde se fait quasiment selon la verticale, de l’émetteur vers le fond marin, puis, après réflexion, du fond marin vers le récepteur.

L’émetteur émet d’abord des ultrasons sinusoïdaux de fréquence f = 20 kHz en « continu » ; la longueur d’onde dans le milieu marin est alors l = 7,5 cm.

En déduire la célérité des ondes ultrasonores dans ce milieu.

l = c/f soit c = l f = 7,5 10^-2*20 000 = 1,5 10³ m/s.

En utilisation « normale », l’émetteur produit ces ultrasons par salves : la durée d’une salve est de 10 ms et elles sont émises à la cadence d’une salve par seconde. Les figures A₁ et A₂ suivantes reproduisent l’allure du signal émis : sur la figure A₁ on visualise deux salves S₀ et S₁ et sur la figure A₂ le détail d’une salve. A partir des données fournies dans le texte, déterminer les valeurs numériques des durées T, T₁ et T₂ indiquées sur ces figures. Justifier, le cas échéant, par des calculs.

T₂ = 10 ms : durée d'une salve.

T₁= 1 s : durée séparant deux salves conséqutives.

T = 1/f avec f = 20 000 Hz ; T = 1/20 000 = 5 10^-5 s.

Proposer une explication pour l’existence d’échos multiples consécutifs à l’émission d’une salve.

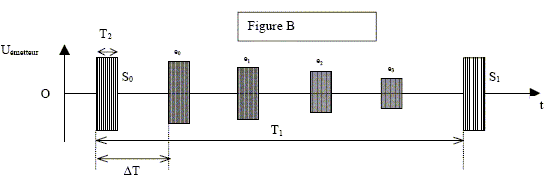
L'onde réfléchie sur le fond, remonte vers l'émetteur ; elle subit une nouvelle réflexion sur la surface de l'océan ( dans la mesure où les vagues ne sont pas trop importantes). L'onde réflichie par la surface atteint le fond sur lequel elle subit une nouvelle réflexion. Et ainsi de suite....

L'existence d'échos multiples est due à ces réflexions multiples sur le fond et la surface.

Pourquoi leur amplitude décroît-elle ?

Lors des réflexions successives l'onde perd de l'énergie : l'amplitude des échos diminue.

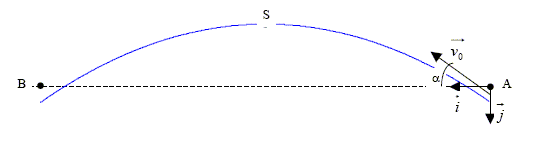
Sauf indication contraire, les mouvements sont décrits dans le référentiel terrestre supposé galiléen.

Un Airbus « zéro g » décrit dans le plan vertical, une portion de trajectoire parabolique pendant 20 secondes. Tout se passe alors comme si le poids était la seule force exercée sur l’avion. L’avion amorce sa trajectoire parabolique en A, avec une vitesse v₀ formant un angle a = 45° avec l’horizontale, il s’élève, franchit le sommet S de la parabole puis suit encore la parabole jusqu’en B, situé à la même altitude que A, avant de redresser sa direction en quittant la parabole.

On munit le plan de la parabole d’un repère orthonormal (A,i,j), i étant horizontal et j vertical descendant. L’avion est repéré par les coordonnées x et y de son centre d’inertie G. On suppose que dans la région où évolue l’avion, le champ de pesanteur est uniforme, de valeur g = 10 m.s^-2.

Faire un bilan complet des forces appliquées à l’avion.

"Tout se passe alors comme si le poids était la seule force exercée sur l’avion"

Poids : appliqué au centre de gravité de l'avion, verticale, vers le bas, valeur P=mg.

Dans la réalité, il faut tenir compte de la portance ( verticale vers le haut), de la traînée et des forces de frottements sur les couches d'air.

Qu’est ce qu’une chute libre ?

Un corps est en chute libre lorsqu'il n'est soumis qu'à son poids.

L’avion est-il en réelle chute libre pendant sa trajectoire parabolique ?

Si le poids est la seule force appliquée à l'avion, ce dernier est en chute libre ( avec vitesse initiale) au cours de sa trajectoire parabolique.

Le pilote a-t-il dû « couper totalement les gaz » pour que l’avion suive cette trajectoire ?

Un mobile soumis uniquement à son poids et possédant une vitesse initiale ( non colinéaire au poids), décrit une trajectoire parabolique.

Les moteurs de l'avion ne sont pas utiles pour suivre cette trajectoire : ils fonctionnent de telle manière que la portance s'annule.

Quelles sont les coordonnées du vecteur accélération du centre d’inertie de l’avion ?

La seconde loi de Newton s'écrit :

accélération : abscisse : 0 ; ordonnée g.

Quelles sont les coordonnées du vecteur vitesse initiale v₀ ?

v₀cos a ; - v₀ sin a.

Etablir les équations horaires du mouvement du centre d’inertie G de l’avion en fonction des paramètres g, v₀ et a (l’instant du passage par A est considéré comme l’instant initial t = 0)

La vitesse est une primitive de l'accélération, d'où les coordonnées du vecteur vitesse : v₀cos a ; gt- v₀ sin a.

La position est une primitive de la vitesse d'où les coordonnées du vecteur position :

x = v₀ cos a t (1) ; y = ½gt²-v₀ sin at. (2)

Démontrer que la trajectoire est bien parabolique dans ces conditions.

(1) donne t =  x /( v₀ cos a) ; repport dans (2) : y = ½gx²/( v₀ cos a)²- tana x.

Il s'agit bien de l'équation d'une branche de parabole.

En déduire l’expression de la vitesse v₀ en fonstion de g, a et t_S.

Au sommet de la parabole, la tangente ( donc la vitesse) est horizontale. La composante verticale de la vitesse est nulle

gt- v₀ sin a =0 soit v₀ = gt_S/ sin a.

Effectuer l’application numérique (on prendra 2^½= 1,4 pour simplifier les calculs)

v₀ = 10 *10 / 0,7 =143 m/s = 1,4 10² m/s.

Calculer l’altitude du sommet S en sachant que celle du point A vaut 9000 m.

y_S = ½gt_S²-v₀ sin at_S = 5*100-143*0,7*10 = 500-1000= -500 m

L'altitude de S est 500 m au dessus de celle de A soit 9500 m.

Calculer la distance entre les positions A et B.

x_B = v₀ cos a t avec t = 20 s ; x_B =143*0,7*20 = 2,0 10³ m.

A l’instant où l’avion amorce sa trajectoire parabolique, un des passagers lâche le stylo qu’il tenait entre les doigts.

Quel est le mouvement ultérieur du centre d’inertie du stylo dans le référentiel terrestre ?

Justifier en tenant compte de la remarque suivante : à l’instant où le stylo est lâché, il possède par rapport au référentiel terrestre, une vitesse égale à celle de l’avion.

Le mouvement du stylo, dans le référentiel terrestre, est le même que celui de l'avion : le stylo est animé de la même vitesse initiale v₀ et le stylo est en chute libre.

Décrire le mouvement du centre d’inertie du stylo dans le référentiel lié à l’avion.

Dans un référentiel lié à l'avion, le stylo est immobile car il tombe à la même vitesse que l'avion.

Quelle sensation peut éprouver le passager s’il a détaché sa ceinture ?

Le passager a l'impression de flotter.

A Quoi sert un tel vol ?

Un vol parabolique permet d'obtenir les conditions d'apesanteur durant une dizaine de secondes : on peut ainsi réaliser des expériences de courte durée en microgravité.

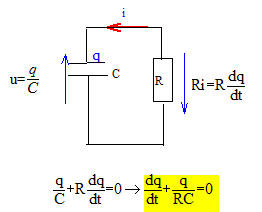
On relie un condensateur de capacité C= 200 / ln 100 mF, préalablement chargé sous la tension E (E = 20 V), à un conducteur ohmique, de résistance R = 100 O.

A partir d’un schéma clair, faisant intervenir la charge q du condensateur, déterminer l’équation différentielle portant sur l’évolution temporelle de q(t).

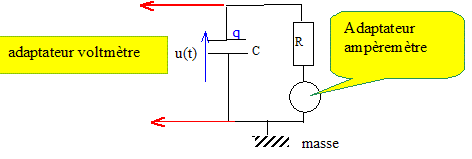
Vérifier que q=Q₀ exp(-t/t) en est solution. En déduire l’expression de la constante t, puis donner celle de Q₀.

dq/dt = -Q₀/t exp(-t/t) ; repport dans l'équation différentielle :

-Q₀/t exp(-t/t) + 1/(RC)Q₀exp(-t/t) = 0 ; -1/t + 1/(RC) = 0 ; t = RC.

à t=0, le condensateur est chargé et la tension à ses bornes vaut E : Q₀ = CE.

Donner l’expression de i(t), intensité circulant lors de la décharge, puis celle de u(t), tension aux bornes du condensateur, en fonction de E, R, C et t.

i(t) = dq/dt = -Q₀/(RC) exp(-t/(RC)) = -CE/(RC) exp(-t/(RC)).

i(t) = -E/R exp(-t/(RC)).

u(t) = q(t) / C ; u(t) = E exp(-t/(RC)).

En vous aidant d’un schéma sur lequel vous indiquerez les branchements à effectuer, expliquer avec quel matériel et comment on peut suivre l’évolution temporelle de u(t) et de i(t).

Utiliser une interface, un ordinateur et un logiciel d'acquisition de données.

On définit l’arrêt de décharge lorsque q=0,01 Q₀. Le condensateur est alors considéré comme totalement déchargé.

Si l’on veut que la décharge s’effectue en 1 s, quelle valeur R’ faut-il donner à la résistance ?

q=Q₀ exp(-t/t) donne : 0,01 Q₀ = Q₀ exp(-1/t) ; 0,01 = exp(-1/t)

ln 0,01 = ln ( 1 / 100 )= -1/t = -1/(R'C) ; ln 100 = 1/(R'C) ; R' = 1/(C ln 100)

Or C= 200 / ln 100 mF = 200 10^-6 / ln 100 F = 2 10^-4 / ln 100 F

R'=1/(C ln 100) = 1/2 10^-4 = 5000 W.

Donner l’expression de l’énergie W₀ initialement emmagasinée dans le condensateur en fonction de C et E.

W₀ = ½CE².

Déterminer en fonction de C et E l’expression de l’énergie perdue par effet Joule dans le conducteur ohmique (R = 100 W) tout au long de la décharge.

Energie perdue par effet joule durant la durée très petite dt : Ri²dt = R E²/R² exp(-2t/(RC))dt = E²/R exp(-2t/(RC))dt.

Puis intégrer entre t=0 et l'infini.

E_J = -½E²C [exp(-2t/(RC))]₀^oo =-½E²C [0-1]

E_J =½CE².

Conclure.

L'énergie initialement stockée dans le condensateur est convertie totalement en énergie thermique dans le résistor.