Pile : sens d'évolution, composition finale du système ; conductivité : solution d'ammoniac concours kiné EFOM 2008

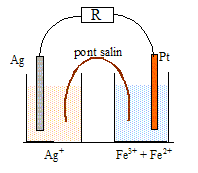
Les couples en présence sont Ag+(aq)/Ag(s) et Fe3+ (aq) / Fe2+(aq). La constante d'équilibre de la réaction Ag+(aq)+Fe2+(aq) =Fe3+ (aq) +Ag(s) vaut K = 3,1. L'électrode de platine n'intervient pas dans les réactions. Le volume des demi-piles est V=1,0 L. Déterminer le sens d'évolution du système, si initialement [Ag+]i = 0,10 mol/L ; [Fe2+]i = 0,010 mol/L ; [Fe3+]i = 0,020 mol/L. Quotient initial : Qr, i = [Fe3+]i / ([Ag+]i [Fe2+]i ) = 0,02 /(0,1*0,01) =2/0,1 = 20. Qr, i > K, le système évolue dans le sens indirect, de la droite vers la gauche. En déduire les réactions aux électrodes et le sens de circulation des électrons dans la résistance R.  Ag(s) = Ag+(aq)+ e- ; oxydation de l'argent à l'anode négative. Fe3+ (aq) +e- = Fe2+(aq); réduction de l'ion fer (III) sur le platine. Les électrons se déplacent de l'argent vers le platine dans le circuit extérieur.   Dresser un tableau descriptif de l'évolution du système. avancement (mol) Ag(s) +Fe3+ (aq) = Fe2+(aq) + Ag+(aq) initial 0 n 0,02 0,01 0,1 en cours x n-x 0,02-x 0,01+x 0,1+x fin xf n-xf 0,02-xf 0,01+xf 0,1+xf Etablir la relation entre xf et K. K = (0,02-xf) / [(0,01+xf)(0,1+xf) ; (0,01+xf)(0,1+xf)K = 0,02-xf. Non demandé {10-3 +0,11 xf + xf2 = 0,02/3,1 -xf/3,1. xf2 + 0,4326xf -5,45 10-3 =0 ; D½ = 0,457 ; xf1 = 1,2 10-2 ; xf2 = -0,44 }. On démontre que xf vérifie une équation du second degré dont les deux solutions sont : -0,44 et 0,012. Justifier votre choix. L'avancement est positif : la valeur -0,44 est à écarter ; xf doit être inférieur à xmax, c 'est à dire à 0,02 mol : la valeur xf = 0,012 mol est à retenir. Calculer les concentrations dans les deux demi-piles quand la pile est usée. La pile est usée lorsque le quotient de réaction, final, est égal à la constante d'équilibre K. avancement (mol) Ag(s) +Fe3+ (aq) = Fe2+(aq) + Ag+(aq) fin xf n-xf 0,02-xf 0,01+xf 0,1+xf 0,012 8,0 10-3 2,2 10-2 0,11 Les volumes de chaque solution étant V=1 L, on peut confondre concentrations et quantités de matière.   Exprimer la quantité de matière d'électrons ayant circulé dans le circuit en fonction de xf et du volume des demi-piles. Fe3+ (aq) +e- = Fe2+(aq). xf V mol d'ion fer (III) se réduit ; la quantité de matière d'électrons est xf V = xf mol car V=1 L. En déduire la quantité d'électricité ayant circulé. 1F~ 105 C. Q = quantité de matière d'électrons fois 1 faraday ; Q = xf * 105 =0,012 *105 = 1,2 103 C. Calculer la variation de masse de l'électrode d'argent. M(Ag)~110 g/mol. Ag(s) = Ag+(aq)+ e- : la masse d'argent diminue de xf mol. |Dm| = xf M(Ag) = 0,012*110 = 1,2*1,1 = 1,3 g. Conductivité : solution d'ammoniac. On dissout 10-3 mol d'ammoniac NH3 aq dans 1 L d'eau. La conductivité de la solution obtenue est égale à 3,2 mS m-1. Déterminer la concentration initiale en ammoniac de la solution. [NH3 aq]i = n/V = 10-3 mol/L = 1 mol m-3. Ecrire l'équation de la réaction de l'ammoniac avec l'eau. Couples acide base : NH3 aq / NH4+ aq ; H2O /HO-aq. NH3 aq +H2O = NH4+ aq +HO-aq. Dresser le tableau d'avancement et déterminer l'avancement maximal. avancement (mol) NH3 aq +H2O = NH4+ aq +HO-aq initial 0 10-3 solvant en large excès 0 0 en cours x 10-3 x x fin ( si réaction totale) xmax 10-3- xmax xmax xmax 10-3- xmax = 0 donne : xmax =10-3 mol.   En utilisant la valeur de la conductivité de la solution, calculer la concentration en ion hydroxyde de la solution. On néglige la conductiité due aux ions oxonium présents dans la solution. lNH4 + = 7,3 mS m2 mol-1 ; lHO- = 20 mS m2 mol-1. s = lNH4 +[NH4+ aq]f + lHO- [HO- aq]f avec [NH4+ aq]f =[HO- aq]f . s = (lNH4 ++ lHO-)[HO- aq]f ; [HO- aq]f = s / (lNH4 ++ lHO-) = 3,2 /(7,3+20) = 3,2 / 27,3 = 0,117 ~0,12 mol m-3 = 1,2 10-4 mol/L. Calculer l'avancement final xf de cette réaction. [HO- aq]f =xf/V avec V= 1 L ; xf = 1,2 10-4 mol Calculer le taux d'avancement final de cette réaction. t = xf/xmax = 1,2 10-4 / 10-3 = 0,12 ( 12%).

retour -menu