Dipôle RC ; datation au carbone 14 concours kiné EFOM 2008

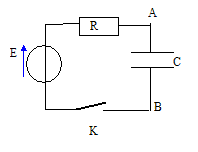
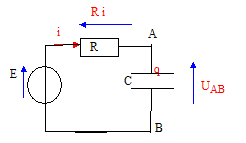
E = 10 V ; R = 1,0 kW. Etablir l'équation différentielle à laquelle satisfait la tension uAB(t) aux bornes du condensateur. Additivité des tensions : E = Ri + uAB(t) avec i = dq/dt et q = CuAB(t) d'où i = CduAB(t)/dt. E = RCduAB(t)/dt + uAB(t) duAB(t)/dt + 1/(RC)uAB(t) = E/(RC)et en posant t =RC il vient : duAB(t)/dt + 1/t uAB(t) = E/t. (1)   Vérifier que la fonction uAB(t) = E[1-exp(-t/(RC))] est solution de l'équation différentielle. Dériver par rapport au temps et remplacer RC par t : duAB(t)/dt = E/t exp(-t/t ) ; repport dans (1) : E/t exp(-t/t ) + E/t[1-exp(-t/t )] = E/t E/t exp(-t/t ) + E/t - E/t exp(-t/t ) = E/t est vérifiée quel que soit t.   Le condensateur possède une tension uAB(t) = 6,3 V au bout de 10 ms. En déduire en justifiant la valeur de la capacité C. A t = 0,10 ms la tension aux bornes du condensateur atteint 63 % de sa valeur finale E= 10 V : donc t = 0,10 ms = 10-4 s. de plus t = RC avec R = 103 W d'où C = t / R = 10-4 / 103 = 1,0 10-7 F. Quelle est la valeur de la tension uAB(t) à t = 1 ms Justifier. En déduire l'énergie emmagasinée dans le condensateur à cette date. Donnée : e-10 = 5 10-5. t/t = 1 /0,1 = 10 ; exp(-t/t ) = e-10 = 5 10-5. par suite uAB(t) = E(1- 5 10-5) ~ E = 10 V. Energie emmagasinée : ½CE2 = 0,5 *10-7*100 = 0,5 10-5 = 5 10-6 J. Donner l'expression de l'intensité du courant i(t) et en déduire sa valeur quand t devient très grand. i(t) = CduAB(t)/dt. i(t) = CE/t exp(-t/t ) = E/R exp(-t/t ). Quand t devient grand par rapport à t, l'exponentielle tend vers zéro : donc l'intensité finale est nulle lorsque le condensateur est chargé.   Datation par le carbone 14. Dans la nature le carbone 14 existe sous forme de deux noyaux isotopes 126C et 146C. Dans la haute atmosphère un neutron formé par l'action des rayons cosmiques bombarde un noyau d'azote 14 ( Z=7) qui se transforme en carbone 14 radioactif b- avec émission d'une autre particule. Tant que la matière est vivante, les échanges de l'organisme animal ou végétal impliquant le dioxyde de carbone atmosphèrique font que le rapport N(146C) / N(126C) est constant. A la mort de l'être vivant, la fin des échanges entraîne la décroissance de ce rapport. Donner la composition des noyaux 126C et 146C. Comment appelle t-on de tels noyaux ? 126C : 6 protons et 12-6 = 6 neutrons ; 146C : 6 protons et 14-6 = 8 neutrons. 126C et 146C sont isotopes. Ecrire l'équation nucéaire correspondant à la réaction d'un neutron sur un atome d'azote. 147N + 10n = 146C + AZX. conservation du nombre de nucléons : 14+1 = 14 +A d'où A= 1 conservation de la charge : 7+0 = 6 + Z doù Z= 1 ( élément hydrogène) 147N + 10n = 146C + 11H. Quel est la nature du rayonnement b- ? électron 0-1e. Ecrire l'équation nucéaire correspondant à la désintégration du carbone 14 en azote 14. 146C = 147N + 0-1e. Qu'appelle t-on période ou demi-vie t½ ? Durée au bout de laquelle l'activité initiale est divisée par deux. Durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. Dans un échantillon de bois vivant, on détecte un atome de carbone 14 pour 1012 atomes de carbone 12. Dans un morceau de bois ancien, mort, on constate qu'il n'y a plus qu'un atome de carbone 14 pour 8 1012 atomes de carbone 12. Quel est l'âge de ce morceau de bois mort ? Donnée : demi-vie du carbone 14 : t½ ~5000 ans. Calcul du rapport N(146C) / N(126C) : Bois vivant : 1/ 1012 = 10-12. Bois mort : 1/ 8 1012 = 0,125 10-12 c'est à dire 8 fois plus petit que la valeur correspondant au bois vivant. A t = t½, ce rapport serait : 0,5 10-12 ; à t =2 t½, ce rapport serait : 0,25 10-12 ; à t =3 t½, ce rapport serait : 0,125 10-12. donc âge du bois mort : 3 *5000 = 15 000 ans.

retour -menu