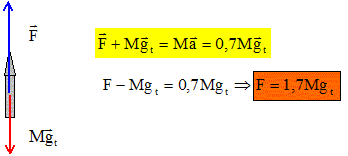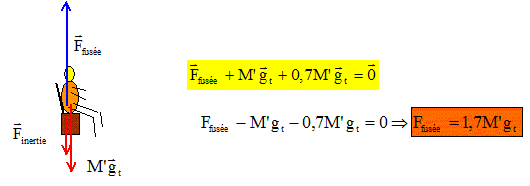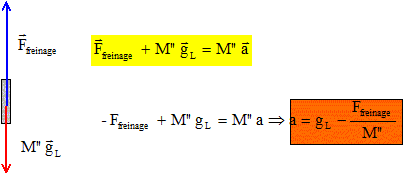Seconde loi de newton ; théorème de l'énergie cinétique concours kiné EFOM 2008

Une fusée ayant, au départ, la masse totale M= 100 t, quitte verticalement la terre sans vitesse initiale. On néglige la résistance de l'air ; on suppose que le champ de pesanteur terrestre garde la valeur constante gt=10 N/kg ; la masse de la fusée et la force de poussée exercée par les moteurs demeurent pratiquement constantes au cous du mouvement. Quelle doit être la force de poussée des moteurs pour que l'accélération du mouvement de la fusée ait la valeur 0,7 gt ? Référentiel terrestre supposé galiléen ; le système est la fusée.   F = 1,7 * 105 *10 = 1,7 106 N.   Quelles sont la vitesse et l'altitude, par rapport à la terre, atteintes par la fusée après 100 s de fonctionnement des moteurs. On choisit un axe verticale orienté vers le haut. L'origine est le sol terrestre. La vitesse est une primitive de l'accélération et la vitesse initiale est nulle. v = 0,7 gt t ; v100 = 0,7*10*100 = 7,0 102 m/s. La position est une primitive de la vitesse et la position initiale est le sol. z = ½ 0,7 gt t2 ; z = 0,5*0,7*10 * 104 = 3,5 104 m = 35 km.   Un cosmonaute, logé dans le compartiment habitable de la fusée a, équipement compris, la masse M' = 100 kg. Quelle force la fusée exerce-t-elle sur lui durant les 100 premières secondes du mouvement ? Système : le cosmonaute ; référentiel non galilen : la fusée. Le cosmonaute est soumis à son poids ( valeur M'gt), à la force exercée par la fusée et à une force d'inertie centrifuge ( valeur : 0,7 M' gt). Le cosmonaute étant immobile, la somme vectorielle des forces est nulle. Ffusée = 1,7*100*10 = 1,7 103 N.   Le champ de pesanteur lunaire garde la valeur constante gL=1,6 N/kg. Le repère Lune est pratiquement galiléen. On se propose de poser un engin sur la lune. Cet engin de masse M" = 3 t est à 50 km du sol lunaire et sa vitesse par rapport à la lune, de valeur 10 800 km /h, est dirigée vers le sol lunaire, suivant la verticale lunaire ; on freine son mouvement de chute en allumant les rétrofusées. Quelle doit être la force de freinage supposée constante pour que l'engin arrive au sol lunaire avec une vitesse nulle ? Appliquer le théorème de l'énergie cinétique : Variation de l'énergie cinétique : DEc = 0-½M" v2 avec M" = 3000 kg et v = 10800 /3,6 = 3000 m/s. DEc = -0,5*3000 *30002 = -1,5 103 * 9 106 = -13,5 109 J. Le travail du poids est moteur en descente : M"gL h avec h = 50 km = 5 104 m. Le travail de la force de freinage, notée F, est résistant lors de la descente : -F h . La variation de l'énergie cinétique est ègale à la somme des travaux des forces : DEc = M"gL h -Fh ; F = M"gL -DEc /h. F = 3 103*1,6-(-13,5 109 / 5 104) =4,8 103 + 2,7 105= 2,748 105 N~2,7 105 N. Calculer la durée de fonctionnement des rétrofusées. Référentiel lunaire galiléen ; système : l'engin ; axe vertical orienté vers le bas dont l'origine est à l'altitude h=50 km. a = 1,6-27,48 104 / 3 103 = 1,6 - 9,16*10 = 1,6-91,6 = -90 m s-2. La vitesse est une primitive de l'acélération et la vitesse initiale est 3 103 m/s. v = a t +v0 avec v0 = 3 103 m/s et la vitesse au sol est nulle. t = v0 / (-a) = 3000/90 = 300/9 = 100/3 = 33,3 s ~ 33 s.

retour -menu