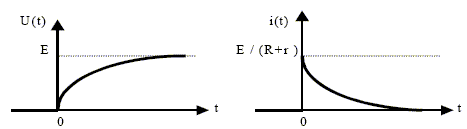Concours d'ingénieurs ECE 2007 ; dipôles RC, RL, LC.

Un circuit électrique comprend un condensateur de capacité C et une résistance électrique R. Le tout est alimenté par un générateur de tension délivrant une tension continue constante U. La charge de ce condensateur est d'autant plus lente que : R est grande Vrai. ( à C constante) C est petite Faux. ( à R constante) U est petite. Faux. ( indépendante de U). La durée de la charge est proche de 5 fois la constante de temps : 5 t =5RC. Pendant la charge, le courant dans le circuit est d'autant plus grand que la différence de potentiel aux bornes du condensateur est grande. Faux. L'intensité du courant décroît au cours de la charge. On considère le dipôle ci-dessous composé d'un condensateur de capacité C et d'une inductance L de résistance interne r nulle. 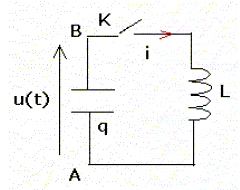L'interrupteur K étant ouvert, le condensateur est chargé initialement à U0=2 V. A l'instant t=0 on ferme l'interrupteur K. On prendra p2=10. Un système d’enregistrement donne la tension u(t) = 2 cos ( 2pt/T) en volt et l'intensité i(t) = -10 sin ( 2pt/T) en mA avec 2p/T= 104 s-1.  On a affaire à des oscillations libres amorties. Faux. Les oscillations sont libres et non amorties ( résistance de la bobine négligeable). La capacité de ce dipôle est C=0,5 mF. Vrai. i(t) = dq(t)/dt = Cdu(t)/dt = -2 104C sin ( 104t) Expression à identifier à -0,01 sin ( 104t) ampère : 2 104C =0,01 ; C= 5 10-7 F=0,5 mF.   La tension u(t) obéit à l’équation différentielle suivante : LC d2u(t) / dt2 + u(t) =0. Vrai. Additivité des tensions : u(t) + Ldi(t)/dt= ; i(t) = dq(t)/dt = Cdu(t)/dt ; di(t)/dt =Cd2u(t) / dt2 L’inductance est L=20 mH. Vrai. LCw2 =1 soit L= 1/(Cw2)=1/( 5 10-7*108)=1/(50)=0,02 H= 20 mH. Un dipôle AB est constitué d'un résistor de résistance R en série avec un condensateur de capacité C(figure ci-dessous). Lorsque l'interrupteur K est en position (1), le dipôle est alimenté par une source de tension de f.é.m. E constante et de résistance r. Les extrémités A et B du dipôle peuvent être court-circuitées en plaçant l'interrupteur en position (2). i(t) désigne l'intensité instantanée du courant dans le dipôle AB et u(t) la tension aux bornes du condensateur. Le condensateur étant initialement déchargé, on place l'interrupteur K en position (1), à l'instant initial t= 0. On s'intéresse à la charge du condensateur. L’équation différentielle liant u(t) et t s’écrit : (R+r)C du(t)/dt -u(t) =E. Faux. Additivité des tensions : E = ri(t) + u(t) +Ri(t) = (R+r) i(t) + u(t). Or i(t) = dq(t)/dt = Cdu(t)/dt d'où : E = (R+r) Cdu(t)/dt + u(t). La résolution de l’équation différentielle conduit à u(t) = E(1-exp(-t/t)) avec t = (R+r)/C. Faux. Il faudrait écrire t = (R+r)C. t caractérise la rapidité de l'évolution temporelle de la tension u(t) pour atteindre le régime permanent. Vrai. Les figures ci-dessous représentent l’évolution de la tension et de l’intensité : Vrai. Au bout d'un temps très long t', on bascule l'interrupteur en position (2). La tension aux bornes de la résistance devient u(t) = E exp(t/t'). Faux. A la décharge du condensateur le courant de décharge est de sens contraire à celui de charge. Additivité des tensions u(t) =Ri(t) ; i(t) = -dq(t)/dt= -Cdu(t)/dt u(t) = -RC du(t)/dt ; u(t) +RC du(t)/dt. solution u(t) = E exp (-t/t') avec t ' = RC. Tension aux bornes du résistor ; Ri(t) = u(t) = E exp (-t/t'). L'expression de i(t) est i(t) = Cdu(t)/dt = -E/R exp(-t/t') avec t'=R/C. Faux. i(t) = -Cdu(t)/dt =-E/R exp (-t/t') avec t ' = RC. La figure ci-dessous représente les fonctions u(t) et i(t) : Vrai. Discontinuité de l'intensité ; continuité de la tension.   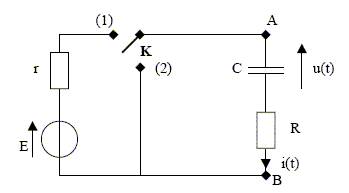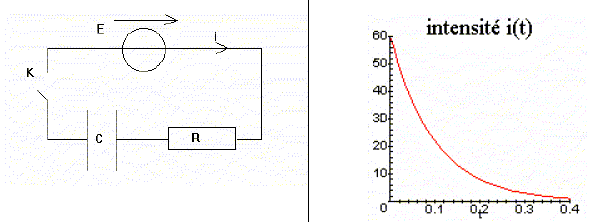On considère un générateur idéal de tension continue, de force électromotrice E=6,0 V, aux bornes duquel on branche, en série, un interrupteur K, un résistor de resistance R = 100 W¶ et un condensateur de capacité C = 1,0 mF. A l'instant t=0, le condensateur est déchargé. L'enregistrement de l'intensité du courant i circulant dans le circuit est donné ci-dessous : le temps t est en ms et l'intensité i(t) en mA. L'ordre de grandeur de la charge q(t) du condensateur au bout d'un temps infini, estimé à partir du graphe est de 6,0 mC. Vrai. qmax= CE = 1*6 = 6,0 mC. L'équation différentielle reliant la charge q(t) du condensateur à l'instant t, est : dq/dt-q/(RC) = E/R. Faux. Additivité des tensions : E = u(t) +Ri(t). Or i(t) = dq(t)/dt et q(t)=Cu(t) d'où : E = q(t)/C +Rdq(t)/dt ; dq(t)/dt+q(t)/ (RC) = E/R. L’équation différentielle a pour solution : q(t) = CE(1-exp(-t/t) avec t =RC. Vrai. q(t) = CE(1-exp(-t/t) corrobore le résultat du graphique. Vrai. i(t) = dq(t)/dt = E/R exp(-t/t) avec E/R = 6/100 = 0,06 A = 60 mA. 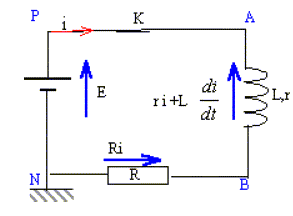Soit le circuit ci-dessous comprenant un générateur de tension idéal E= 20 V, un interrupteur K, une bobine inductive (L=10 mH ; r =10 W) et une resistance R=2 kW . A l'instant t=0 on ferme l'interrupteur K. On fera les approximations : 1990~2000~2010. Juste apres la fermeture de l'interrupteur K, l'intensité du courant dans la résistance est nulle. Vrai. La bobine introduit un retard à l'établissement du courant. Juste après la fermeture de l'interrupteur K, la tension aux bornes de la bobine est égale à 0 V. Faux. additivité des tensions : E = R i + r i + Ldi/dt ; or i(t=0) = 0 d'où E = Ldi/dt. La constante de temps du circuit est t =5 ms. Vrai. t= L/(R+r) = 0,01/(2000+10) ~ 0,01/2000 = 5 10-6 s = 5 ms. L'intensité du courant en régime permanent est I= 5 mA. Faux. I étant constant dI/dt=0 ; E = R I + r I ; I = E/(R+r) = 20/(2000 + 10) ~20/2000 = 0,01 A = 10 mA. 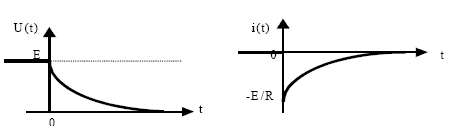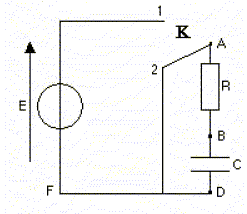Soit le circuit ci-dessous comprenant un générateur de tension idéal E= 10 V, un interrupteur K, un condensateur de capacité C= 10-7 F et une résistance R = 10 kW¶ . Le condensateur est chargé lorsque l'interrupteur est en position 1 puis, à l'instant t=0, on met l'interrupteur sur la position 2.   L'énergie initialement emmagasinée dans le condensateur va être dissipée sous forme calorifique dans le conducteur ohmique de résistance R. Vrai. L'énergie emmagasinée dans un condensateur est Ec(t) = ½Cu2. Vrai. L'energie emmagasinée dans le condensateur à l'instant initial de la décharge est Ec(t=0) = 5 mJ. Vrai. ½CE2 = 0,5 10-7*100 =5 10-6 J = 5 mJ. L'énergie W dissipée par effet Joule dans la résistance R dans le circuit pendant la phase de décharge est W=5 J. Faux. 5 mJ. On considère le circuit représentésur la figure ci-dessous où E= 10V, R = 18 W¶ , L= 1 H et r = 7 W . 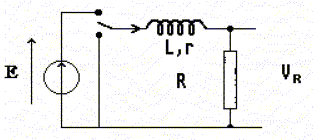¶ On place l'interrupteur en position haute et on mesure, en régime permanent, l'intensité du courant électrique dans le circuit I= 4 A. Faux. En régime permanent I = E/(R+r) = 10/(18+7) = 10/25 = 0,4 A. A l'instant t=0, on place l'interrupteur en position basse et on peut alors écrire i(t) =I0 exp(-t/t) avec t=(R+r)/L. Faux. Additivité des tensions ri + Ldi/dt +Ri =0 ; Ldi/dt + (R+r)i = 0 ; di/dt + (R+r)/L i=0 i(t) = I0 exp(-t/t) avec t = L/(R+r). La tension aux bornes de la résistance R est UR =R I0 exp(-t/t) . Vrai. A t=0 la tension UR est maximale URmax = RI0 , à l'instant t1 la tension chute à 90% de sa valeur maximale et à l'instant t2 la tension est passée à 10% de sa valeur maximale. On note T la durée de la décharge. La durée de la décharge est T =t 2-t1 = t ln9. Faux

retour -menu