|
Physique et médecine, chute d'une bille dans l'air. Concours manipulateur électroradiologie médicale Caen 2008 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Données :
Energie de masse de l'unité de masse atomique 931,5 MeV. Célérité des ondes ultrasonores dans le corps humain : v = 1,5 km/s. A- Echographie médicale : Dans les cliniques ou les hopitaux on peut lire dans les couloirs le nom d'un service appelé échographie. Pour effectuer une échographie on utilise une sonde émettrice et réceptrice d'ultrasons. On admet que les dimensions des détails observés sur une echographie sont de l'ordre de la longueur d'onde ultrasonore employée. Les fréquences utilisées sont de l'ordre de : f1 = 2,0 MHz pour les organes profonds, f2 = 6,0 MHz pour les petits organes et la pédiatrie, f3 =15 MHz pour l'ophtalmologie ( soins des yeux). Pour les trois fréquences, calculer les longueurs d'onde dans le corps humain. l = v/ f ; v = 1500 m/s ; 1 MHz = 106 Hz. l1 = 1500 / 2 106 = 7,5 10-4 m ; l2 = 1500 / 6 106 = 2,5 10-4 m ; l3 = 1500 / 15 106 = 1,0 10-4 m ; Quelles sont les dimensions, notées a1, a2 et a3 ( en mm) des détails que l'on peut observer pour les fréquences utilisées ? a1~7,5 10-4 m~ 0,75 mm ; a2~27,5 10-4 m~ 0,25 mm ; a1~ 10-4 m~ 0,10 mm On admet que la limite de l'observation s'effectue lorsque l'intensité ultrasonore, reçue après réflexion, est la moitié de l'intensité émise. On note D la distance parcourue par l'onde pour laquelle l'intensité de l'onde ultrasonore reçue est la moitié de l'intensité de l'onde émise. D'autre part, si on multiplie par k la fréquence f utilisée, D est divisée par k2. Pour f1 = 2,0 MHz, on a D1 = 6,0 m. Quelle est la profondeur sondée h1 pour la fréquence f1 = 2,0 MHz ? aller + retour = D1 = 2 h1 d'où h1 = ½D1 = 3,0 m. Quelle est la profondeur sondée pour les fréquences de 6,0 MHz et 15 MHz ? Si la fréquence est multipliée par 3, la distance D est divisée par 9 d'où h2 = h1/9 = 3/9 = 0,33 m. Si la fréquence est multipliée par 7,5, la distance D est divisée par 7,52 d'où h3 = h1/7,52 = 3/7,52 = 0,053 m = 5,3 cm Expliquer pourquoi la fréquence f3 ne convient pas pour l'observation d'un organe profond. La fréquence f3 permet seulement l'observation des organes situés à une distance inférieure à 5,3 cm.
Utilisation de l'iode 131 émetteur b- de demi-vie t½=8 jours. Quelle est la nature de la particule b- émise par l'iode 131 lors de sa désintégration ? La particule b- est un électron noté 0-1e. Ecrire l'équation de désintégration de l'iode 131 en utilisant les données. 13153I --> 0-1e + AZX. conservation de la charge : 53 =-1 +Z d'où Z = 54 conservation du nombre de nucléons : 131 =A 13153I --> 0-1e + 13154Xe. Calculer, en MeV,l'énergie libérée par chaque désintégration. Commenter le signe du résultat obtenu. Dm = m(13154Xe) + m( 0-1e ) - m(13153I) = 130,87545-5,4858 10-4 - 130,87705=-1,05142 10-3 u. E= -1,05142 10-3 *931,5 = -0,9794 ~ -0,98 MeV. Le signe moins indique que l'énergie est transférée au milieu extérieur. Pour une scintigraphie thyroïdienne, un patient adulte doit ingérer par voie orale un quantité d'iode 131 d'activité A0. Le délai entre l'administration du traceur et la réalisation des images est de 24 h. Donner l'expression de l'activité A de l'iode 131 dans le corps en fonction de A0, t½ et de t le temps où les images sont réalisées. A = A0 exp(-lt) avec l t½ = ln2 ; ln A0/A = lt = ln2 * t/t½ = ln 2 t/t½. A0/A =2 t/t½ ; A/A0 =2 -t/t½. Calculer A/A0 en % pour t=24 h. t/t½ = 24/(8*24) = 0,125 ; A/A0 =2 -0,125 = 0,917 ( 91,7 %).
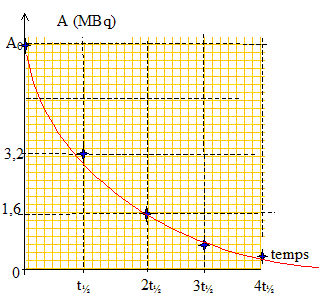
Calculer la constante de temps t en heure et seconde. A = A0 exp(-lt) = A0 exp(-t/t) d'où t = 1/l = t½/ln2 = 13,2/0,693 = 19,044 h~ 19,0 h. t = 19,044*3600 = 6,86 104 s. Pour une scintigraphie thyroïdienne, il faut injecter à un patient adulte une quantité d'iode 123 d'activité A0 = 6,4 MBq. Tracer l'allure de la courbe représentant A en fonction du temps. ( on représentera simplement les activités correspondant à t½, 2t½, 3t½, 4t½, 5t½, )
La réalisation des images se fait entre 2 et 4 heurs après administration de l'iode. Calculer l'activité de l'iode 123 si on réalisait, comme dans le cas de l'iode 131, une image après 24 h d'injection ? Conclure. t/t½ = 24/13,2 = 1,818 ; A/A0 =2 -1,818 = 0,284 ( 28,4 %). A = 0,284 A0 = 0,284*6,4 = 1,8 MBq. L'activité de l'iode 131 est beaucoup trop faible au bout de 24 h pour que l'on puisse réaliser des images interprétables.
Défibrillateur externe : un condensateur pour sauver une vie. Un défibrillateur externe est l'appareil utilisé pour appliquer des chocs électriques à un patient dont le coeur est en fibtilation ( contractions désordonnées des fibres musculaires). Le texte ci-dessous décrit les caractéristiques des appareils dits " à choc exponentiel tronqué". Le circuit destiné à produire un choc exponentiel tronqué est constitué d'un condensateur de stockage d'énergie, du patient et d'un contacteur. Pour générer un choc de 360 J, le condensateur est chargé à un niveau situé entre 1500 V et 2000 V, puis déchargé à travers la cage thoracique du patient durant une période de temps spécifiée. Les spécifications des défibrillateurs externes sont généralement données pour une charge de 50,0 W. Dans cet exercice on considère un appareil pour lequel la tension de charge est U0 = 1,81 kV. On appelle C la capacité du condensateur. On assimilera la cage thoracique du patient à un conducteur ohmique de résistance R= 50,0 W. Le contacteur est un interrupteur permettant de contrôler l'administration du choc. Quelle est la capacité du condensateur à utiliser pour délivrer une énergie de 360 J ? E= ½CU02 ; C= 2 E/ U02 = 2*360/18102 =2,198 10-4 F ~ 2,2 10-4 F. L'expression de l'évolution de la tension aux bornes du condensateur au cours d'un choc est de la forme UC= A exp(-t/t) ou t est la constante de temps du circuit. Que représente A, préciser sa valeur. A = U0 = 1810 V. On rappelle qu'un condensateur est considéré comme déchargé au bout d'un temps t = 5t. Pour la valeur de C précédente, quelle serait approximativement la durée nécessaire pour délivrée une énergie de 360 J ? 5 t = 5 RC = 5*50*2,198 10-4 ~0,055 s = 55 ms. Etablir l'expression en fonction du temps de l'intensité du courant de décharge. q(t) = Cu(t) = CU0exp(-t/t) ; i(t) = dq/dt = CU0(-1/t) exp(-t/t) i(t) = -U0/R exp(-t/t). Quelle est, en valeur absolue, la valeur maximale atteinte par l'intensité au cours du choc ? Cette valeur dépend t-elle de la capacité du condensateur ? Imax = U0 /R =1810/50 = 36,2 A, indépendante de C. Pour la valeur de C précédente, quelle est la valeur de l'intensité à t = 11 ms après le début du choc ? t= t = 11 ms, i(t) = 0,37 Imax = 0,37*36,2 = 13,4 A. Que faudrait-il modifier afin que l'intensité diminue moins vite au cours du choc ? Aumenter U0 ( R étant fixée à 50 W), c'est à dire diminuer C à énergie E=360 J constante.
coefficient de frottement fluide k = 3,12
10-4 S.I g = 9,80 m/s2. masse volumique de l'air : r
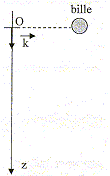
= 1,3 kg m-3. Une bille de masse m=20 g, de rayon R= 2,0 cm est lâchée sans vitesse initiale depuis un point O. Durant sa chute, la bille est soumise à une force de frottement fluide, s'opposant au mouvement, d'intensité f = kv2, où k est le coefficient de frottement fluide et v la vitesse de la bille. Par une analyse dimensionnelle, déterminer l'unité de k. k= force / vitesse2 ; force : N soit kg m s-2 ; vitesse2 : m2 s-2. k s'exprime en kg m-1 ou encore [k]= M L-1. Donner l'expression de la poussée d'Archimède, notée P et calculer sa valeur. Montrer qu'il est raisonnable de négliger cette force. Justifier. P= Vrg = 4/3 p r3 r g = 4/3*3,14*0,023*1,3*9,8 = 4,3 10-4 N. Poids : mg = 0,02*9,8 = 0,196 N. Le poids est bien supérieur à la poussée d'Archimède : celle-ci est négligeable devant le poids. Etablir l'équation différentielle du mouvement. La bille est soumise à son poids ,verticale, vers le bas, valeur mg et à la force de frottement fluide, verticale, vers le haut, valeur kv2. Sur un axe vertical descendant la seconde loi de Newton s'écrit : mdv/dt = mg-kv2 ; dv/dt + k/m v2 = g. dv/dt + 3,12 10-4 /0,02 v2 = 9,8 ; dv/dt + 0,0156 v2 = 9,8. Méthode d'Euler : Le tableau suivant représente un extrait de la feuille de calcul des vitesses (v) et accélération (a) de la bille en fonction du temps.
a3 + 0,0156 v23 = 9,8 ; a3 = 9,8-0,0156*2,932 =9,66 m s-2. v4 = v3 + a3 Dt ; v4 = 2,93 +9,66*0,1 = 3,90 m/s. Exprimer littéralement la vitesse limite que pourrait atteindre la bille si elle ne retombait pas sur le sol puis calculer sa valeur. dv/dt + k/m v2 = g. Quand la vitesse limite est atteinte dvlim/dt=0 soit : v2lim = mg/k ; vlim =[mg/k]½. vlim =[0,02*9,8 /3,12 10-4]½ =25 m/s. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|