Oscillateur élastique, poussée d'Archimède, Kepler, dipôle LC  concours kiné Berck 2008.

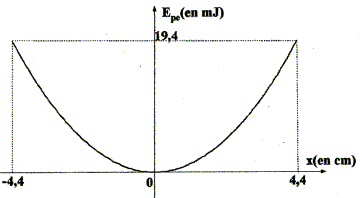
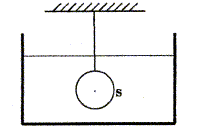
Oscillateur élastique. Texte : un oscillateur est constitué par un solide S de masse m attaché à l'extrémité d'un ressort à spires non jointives, de masse négligeable et de constante de raideur k. Le solide S oscille sans frottement sur un axe horizontal. On repère la position, à la date t, du centyre d'inertie G de S par l'abscisse x. L'origine O du repère correspond à la position du centre d'inertie à l'équilibre. Le graphe suivant donne les variations de l'énergie potentielle élastique de l'oscillateur. m = 136 g Analyse : Question relative à la raideur du ressort. L'amplitude des oscillations est égale à : xmax = 4,4 cm = 0,044 m. Lorsque x=xmax = 4,4 cm, l'énergie de l'oscillateur est sous forme potentielle élastique : ½kx2max = 19,4 10-3 J k = 2* 19,4 10-3 / 0,0442 ; k = 20 N/m. Question relative à la période. T = 2p [m/k]½. avec m = 0,136 kg T = 2*3,14 [0,136/20)½ ; T = 0,52 s = 520 ms. Question relative à la vitesse maximale. Au passage à la position d'équilibre, l'énergie est sous forme cinétique : ½mv2max = 19,4 10-3 J vmax = ( 2* 19,4 10-3 / 0,136)½ ; vmax = 0,53 m/s. Question relative à l'accélaration maximale du solide. x(t) est de la forme x(t) = xmax cos (wt) avec w = 2p/T = 6,28/0,52 =12,1 rad/s La vitesse est la dérivée de x(t) par rapport au temps : v(t) = x'(t) = -xmaxwsin (wt) L'accélération est la dérivée de la vitesse par rapport au temps : a = x"(t) = -xmaxw2cos (wt) La valeur maximale de l'accélération est : xmaxw2 = 0,044*12,12 =6,5 m/s2.   Poussée d'Archimède. Texte : une sphère de porcelaine de diamètre D = 30 mm est accrochée à un fil inextensible et de masse négligeable. Cette sphère est immergée dans l'éthanol. densité de l'éthanol : d= 0,79 ; masse volumique de la porcelaine : m = 2,3 g/cm3. Analyse : Question relative à la tension (N) du fil. ( 0,21 ; 0,42 ; 0,57 ; 0,68 ; 0,92 ; aucune réponse exacte ) Volume de la sphère de rayon R= 15 mm = 1,5 cm : V = 4/3pR3 = 4/3*3,14*1,53 =14,13 cm3. masse de la porcelaine : m = Vm = 14,13*2,3 =32,5 g = 0,0325 kg Poids de la sphère :P=mg = 0,0325*9,81 =0,319 N Poussée d'Archimède : F = Vdg = 14,13*0,79 *9,81 = 109,5 mN = 0,1095 N La tension du fil est égale au poids apparent, c'est à dire au poids diminuée de la poussée : T = 0,319-0,1095 =0,21 N.   3è loi de Kepler. Analyse : Question relative au référentiel. Dans le référentiel héliocentrique, la trajectoire du centre d'une planète est une ellipse dont le soleil occupe l'un des foyers. Dans le référentiel géocentrique, le mouvement du centre d'une planète est quelconque. D'ailleurs ce référentiel est utilisé pour l'étude des mouvements des satellites de la terre. Question relative à la période. La 3è loi de Kepler s'écrit : T2/R3 = Cte ou T2 = Cte * R3 . Le périodes des planètes les plus éloignées du soleil ont donc des périodes de révolution plus grandes que celles qui en sont proches. La période d'un satellite est indépendante de sa masse. Question relative à la constante de gravitation G. F= GMm/d2 soit G = F d2/(Mm) L'unité de G est : N m2 kg-2. Question relative à la vitesse. v = (GM/a)½ avec a demi grand axe de l'ellipse. La vitesse est d'autant plus petite que la distance a est grande ( qu'une planète est plus éloignée du soleil ). dipôle LC. 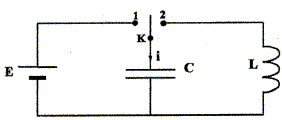Texte : L'interrupteur est en position 1 ; on charge le condensateur de capacité C=10 mF par le générateur de fem E et de résistance interne négligeable. On bascule l'interrupteur en position 2. Le condensateur chargé est relié à une bobine d'inductance L et de résistance négligeable. On prendra comme origine des temps l'instant où l'on bascule l'interrupteur en position 2. L'intensité du courant est une fonction sinusoïdale du temps qui s'écrit : i(t) = -57 10-3 sin (8,2 102 t). Les unités dans cette formule sont celles du système international. Analyse : Question relative à la valeur E ( V) de la fem du générateur. Energie initiale du générateur chargé : ½CE2. On observe un échange permanant d'énergie entre condensateur et bobine. Energie maximale stockée par la bobine : ½LI2max. Par suite : ½CE2 = ½LI2max ; CE2 =LI2max avec C = 10-5 F et Imax = 57 10-3 A E = L½ Imax C-½ = L½ 57 10-3* 316,22 ; E = 18,024 L½. (1) Période de cet oscilateur électrique T = 2p(LC)½ = 2p/ w d'où w = (LC)-½ De plus w = 8,2 102 rad/s d'après l'expression de l'intensité. 1/8202 = LC soit L = 1,487 10-6 / 10 10-6 = 0,1487 H. Repport dans (1) : E = 18,024 *0,1478½ =6,95 V ( E = 7,0 V)

retour -menu