Projectile concours kiné Berck 2008

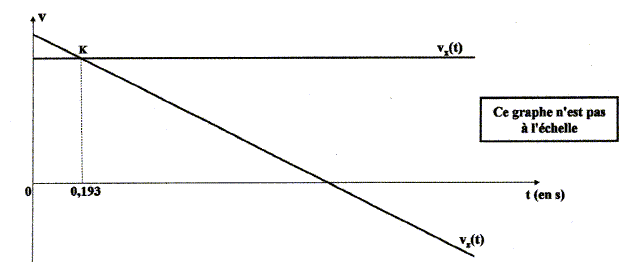
Projectile. On lance un projectile de masse m, considéré comme ponctuel, à partir d'un point A, à la vitesse v0 faisant un angle a avec l'horizontale. A la date t=0, le projectile est en A. Le graphe ci-dessous donne l'allure des représentations graphiques des coordonnées vx(t) et vz(t) de la vitesse en fonction du temps.     Au point K les coordonnées vx(t) et vz(t) de la vitesse sont égales. A l'instant tK=0,193 s, le projectile se situe au point K de coordonnées xK= 1,31 m et yK= 5,67 m. Les frottements sont négligés.   Les vecteurs sont écrits en gras et en bleu. Déterminer la valeur de l'angle a (°). accélération a ( 0 ; -g) ; vitesse initiale : v0 ( v0 cos a ; v0 sin a ) ; position initiale : OA ( 0 ; h) La vitesse est une primitive de l'accélération : v ( v0 cos a ; -gt + v0 sin a) Au point K, vx(t) =vz(t), d'où : v0 cos a = -gt + v0 sin a) v0 cos a = -9,81*0,193 + v0 sin a. v0 cos a = -1,893+ v0 sin a ; v0 ( sin a- cos a)= 1,893 (1) La position est une primitive de la vitesse : x(t) = v0 cos a t (2) ; z(t) = -½gt2 + v0 sin a t + h. (3)   Au point K (2) donne : v0 cos a =xK/tK =1,31/0,193 ; v0 cos a = 6,787. (4) Au point K (3) donne : 5,67 = -0,5 *9,81*0,1932 +v 0 sin a *0,193 + h 5,67 + 0,1827 = 0,193 v 0 sin a + h ; 5,853 = 0,193 v 0 sin a + h v 0 sin a = (5,853 -h ) / 0,193 = 30,32-5,181 h (5) Repport dans (1) : 30,32-5,181 h -6,787 = 1,893 5,181 h =21,64 ; h = 21,64 / 5,181 = 4,177 m ( h = 4,18 m). (5) s'éccrit : v 0 sin a =30,32 - 5,181 * 4,177 ; v 0 sin a =8,68. (5) / (4) s'éccrit : tan a = 8,68 / 6,787 =1,279 soit a =51,98° ( a =52°) En déduire la valeur de v0. (4) donne v0 = 6,787 / cos a = 11,02 m/s. (v0 =11,0 m/s) Calculer la valeur de h en mètre ? h = 4,18 m.   Déterminer la valeur de zS. Au sommet de la trajectoire, la vitesse est horizontale : la composante verticale de la vitesse est donc nulle. -gt + v0 sin a = 0 soit t = v0 sin a / g Repport dans z(t) : z(t) = -½gt2 + v0 sin a t + h. zS= -½g(v0 sin a / g)2 + (v0 sin a)2 / g +h zS=(v0 sin a)2 / (2g) +h. zS= (11*sin 52)2/(2*9,81) + 4,18 zS= 8,0 m.  Déterminer la valeur de xP. Il faut d'abord déterminer la date t P. zP(t) =0= -½gtP2 + v0 sin a tP +h. -0,5 *9,81 tP2 +11*sin 52 tP +4,18 =0 ; -4,905 tP2 +8,668 tP +4,18 =0 tP2 -1,767tP -0,852 =0 ; tP = 2,161 s Repport dans x(t) = v0 cos a t (2) xP = 11*cos52 * 2,161 ; xP =14,6 m.

retour -menu