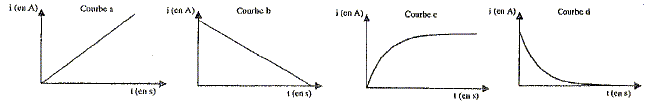Circuit RL et RLC examen d'admission audioprothesiste Rennes 2008.

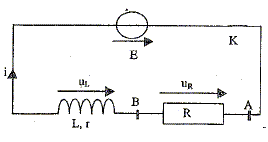
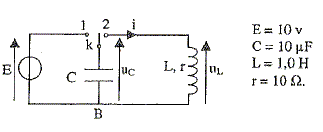
L'objectif de cette étude est de trouver expérimentalement la capacité d'un condensateur et l'inductance d'une bobine pour les comparer à celles données par le fabricant. Le matériel disponible est le suivant : Bobine d'inductance L= 1 H et de résistance r= 10 W; condensateur de capacité C= 10 mF générateur de tension constante E= 10 V ; conducteur ohmique de résistance R= 1 kW ; interrupteur, fils de connexion ; système d'acquisition. 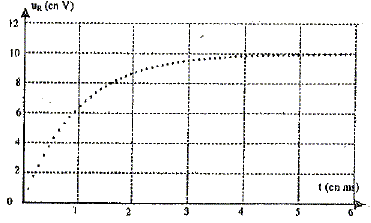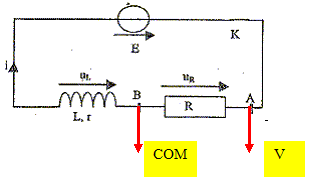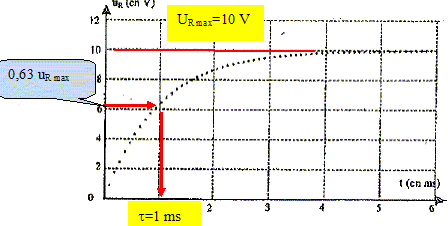Etude expérimentale d'un circuit RL : Le schéma du montage est représenté ci-dessous ( le système d'acquisition n'est pas représenté) : Une fois le paramètrage du système d'acquisition effectué, on ferme l'interrupteur à l'instant t=0 et on enregistre l'évolution de la tension aux bornes du conducteur ohmique de résistance R en fonction du temps. On obtient l'enregistrement suivant : L'adaptateur du système d'acquisition s'utilise comme un voltmètre. Il possède deux bornes : COM et V. Préciser à quel points du circuit il faut relier ces bornes pour obtenir la courbe ci-dessus. Pour visualiser la tension UAB, B est relié à la borne COM. On donne différentes courbes susceptibles de représenter l'intensité du courant en fonction du temps. Choisir celle qui correspond à l'évolution de l'intensité et justifier. La tension aux bornes d'un conducteur ohmique et l'intensité qui le traverse sont proportionnelles : l'image de l'intensité est semblable à celle de la tension UAB ( courbe expérimentale donnée ci-dessus) au facteur R près. Donc courbe c. Quelle est l'influence de la bobine sur l'établissement du courant lors de la fermeture du circuit ? La bobine inductive introduit un retard à l'établissement du courant à la fermeture du circuit. Modélisation et équation différentielle. Si la résistance r de la bobine est négligeable devant R, montrer que l'équation différentielle de ce circuit, interrupteur fermé, peut s'écrire : E= uR + L/R duR/dt . Additivité des tensions : tension aux bornes de la bobine : uL= Ldi/dt + ri ~ Ldi/dt tension aux bornes du résistor : uR = R i R en ohms; L en henry ; intensité en ampère et tension en volt. E= uL+ uR =Ldi/dt +Ri ; or i = uR / R et di/dt = 1/R duR/dt. E= L/R duR/dt +uR. équation différentielle à la fermeture de l'interrupteur. ULe terme L/R correspond à la constante de temps t de ce circuit.  Par une analyse dimensionnelle, montrer que cette constante a la dimension d'un temps. Ldi/dt à la dimension d'une tension donc L à la dimension : [V] [T] [A]-1. R est en ohm , une tension divisée par une intensité : [V] [A]-1. L/R a la dimension : [V] [T] [A]-1 [A] [V]-1=[T]   . On note uR(t) la valeur prise par la tension uR à l'instant t=t. Sachant que uR(t) = 0,63 uR max, déterminer à partir du graphe la valeur de la constante de temps de ce circuit. En déduire la valeur de L et la comparer avec l'indication du fabricant. t= L/R avect = 10-3 s et R = 1000 W. L = t R = 10-3 *1000 = 1 H, en accord avec l'indication du fabricant. Etude du circuit oscillant. 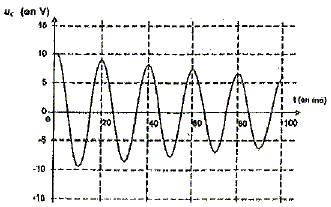On réalise ensuite le montage ci-dessous : On bascule l'interrupteur en position 1 pour charger le condensateur puis on le bascule en position 2. Avec le même système d'acquisition et de traitement, en adaptant le paramètrage, on enregistre la tension uC(t) dont le graphe est représenté ci-dessous : Comment peut-on expliquer la diminution de l'amplitude des oscillations au cours du temps ? Au cours des échanges d'énergie entre condensateur et bobine, une partie de celle-ci est dissipée en chaleur dans les parties résistives : il en résulte un amortissement des oscillations.   Déterminer la valeur de la pseudo-période T du signal. 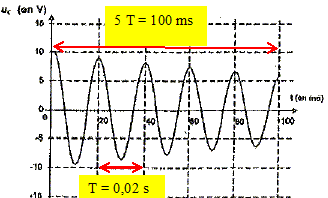On peut considérer dans ce cas que la période et la pseudo-période ont la même valeur. En déduire la valeur de la capacité C du condensateur et la comparer avec l'indication du fabriquant. On donne p2~10. T = 2p (LC)½ ; C =4p2 / T2L) avec L~ 1 H C = 4*10 / (4 10-2)2 =10/10-4=10-5 F = 10 mF, en accord avec l'indication du fabricant.

retour -menu