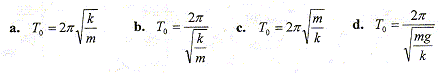Mécanique, dipôle RC. Concours manipulateur électroradiologie médicale APHP 2008.

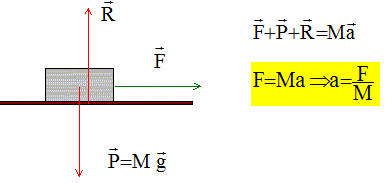
vitesse, accélération. Texte : un système est en mouvement dans le référentiel terrestre considéré comme galiléen. Il est animé d'une vitesse ( vecteur v) dont la direction et le sens varie au cours du temps. A. Le vecteur vitesse est toujours tangent à la trajectoire. vrai. B. L'accélération du système est égale à la variation du vecteur vitesse par unité de temps. vrai. Il faudrait écrire " le vecteur accélération du centre d'inertie " C. Si le système est animé d'un mouvement rectiligne uniforme alors son vecteur accélération a même direction et même sens que le vecteur vitesse. faux. Le principe d'inertie affirme que dans le cas d'un mouvement rectiligne uniforme, le système est pseudo-isolé ( la somme vectorielle des forces est nulle). En conséquence, d'après la seconde loi de Newton, le vecteur accélération est nul. D. Si le système est animé d'un mouvement circulaire uniforme alors son accélération est nulle. faux. Le vecteur accélération est centripète ; sa valeur est a=v2/R, avec R rayon du cercle. accélération. Texte :un objet de masse M= 10 kg se déplace, à partir de la date t=0, suivant une trajectoire rectiligne sur un axe horizontal Ox. Il est soumis à une force F orientée vers les x positifs et de valeur F= 120t + 40 (N). L'expression de son accélération ( en m s-2) à un instant quelconque est :. A.120 ; B. 12t ; C. 12t+4 ; D. 1200t+400 Analyse :  a = 12t+4.   pendule. Texte : un pendule, formé d'une bille de masse m, est attachée à un fil inextensible de longueur L et de masse négligeable. Il est lâché sans vitesse initiale à la date t=0. A. Si l'abscisse angulaire de la bille est inférieure à 10 degrés, la période des oscillations est constante. vrai. Il faudrait préciser " les frottements sont négligeables". B. La période des oscillations dépend de la masse de la bille. faux. T = 2p [L/g]½. C. Si on double la longueur du fil, la période double. faux. T est "proportionnelle à L½" . D. Quand la bille passe par la position d'équilibre, son énergie potentielle de pesanteur est minimale. vrai. En absence de frottement, l'énergie mécanique se conserve. A la position d'équilibre la vitesse, donc l'énergie cinétique, est maximale : l'énergie potentielle est donc minimale Chute verticale. Texte : un solide de masse m est lancé verticalement vers le haut avec une vitesse initiale v0.  A. L'énergie mécanique du système est la somme de l'énergie cinétique et de l'énergie potentielle de pesanteur. vrai. B. L'énergie mécanique du système est constante si les frottements sont négligeables. vrai. C. L'énergie cinétique du système est nulle à la date t=0. faux. La vitesse initiale n'est pas nulle. D. Lorsque le solide atteint son altitude maximale, son énergie cinétique est nulle. vrai.   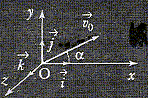Projectile. Texte : Dans le champ de pesanteur uniforme, à la date t=0, on lance du point origine O, une balle de masse m avec une vitesse initiale v0. A. L'expression de la vitesse initiale suivant Ox est : v0 cos a. vrai. B. L'expression de la vitesse initiale suivant Oy est : -v0 sin a. faux. + v0 sin a. C. L'abscisse du centre d'inertie de la balle à la date t est : x = -gt + v0 cos a t. faux. x = v0 cos a t. C. L'ordonnée du centre d'inertie de la balle à la date t est : y = -½gt2+ v0 sin a t. vrai. oscillateur élastique. La période propre T0 d'un oscillateur de masse m et de constante de raideur k est donnée par : b et c sont vrais. Dipôle RC. 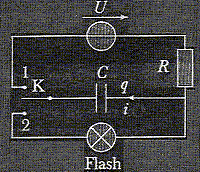On étudie le principe de fonctionnement d'un flash d'un appareil photographique jetable. Un circuit électronique, alimenté par une pile de fem E=1,5 V, permet d'obtenir une tension U= 300 V. Un condensateur de capacité C= 150 mF est chargé à travers un conducteur ohmique de résistance R= 1,00 kW. Ensuite le condensateur se décharge dans le tube du flash de résistance r. 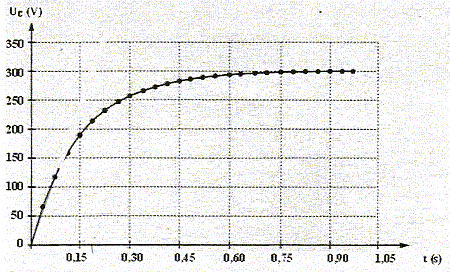Le schéma simplifié du circuit est représenté ci-dessous : A. Exprimer la constante de temps du circuit de charge et déterminer sa valeur. t = RC = 103*150 10-6 = 0,150 s. B. Par analyse dimensionnelle vérifier que la constante de temps est homogène à une durée. R : résistance soit tension / intensité. C : capacité soit charge / tension ou intensité * temps / tension. Par suite RC est un temps. C. Le graphe suivant représente l'allure des variations de la tension aux bornes du condensateur notée uc en fonction de t : Cette courbe concerne t-elle la charge ou la décharge du condensateur ? La tension uc est croissante et tend vers la valeur 300 V : il s'agit de la charge du condensateur. Sur quelle position est l'interrupteur ? Sur la position 1. Indiquer la date t à partir de laquelle le régime devient quasiment permanent. Comparer avec t. Lorsque le régime permanent est atteint, la tension aux bornes du condensateur vaut 300 V. Cette valeur est atteinte à t = 0,75 s soit 5 t. Donner l'expression de l'intensité du courant i dans le circuit à t=0 et sa valeur en régime permanent. additivité des tensions U = Ri + uc. A t=0, le condensateur est déchargé, uc(0)=0, par suite i(0) = U/R = 300/1000 = 0,3 A. En régime permanent uc=U , donc Ri est nulle : i =0. Calculer l'énergie Ec emmagasinée par le condensateur en fin de charge. La comparer à celle que le condensateur aurait stockée s'il avait été chargé par la pile de fem E. Ec= ½CU2 = 0,5*1,5 10-4*3002 = 0,5*1,5*9 =0,75*9 = 6,75 J. Charge directe avec la pile : Ec= ½CE2 = 0,5*1,5 10-4*1,52 = 0,75*2,25 10-4 ~ 1,7 10-4 J. C'est à dire environ 40 000 fois plus faible. Quelle est la puissance électrique moyenne consommée par la lampe du flash si elle éclaire pendant une durée d'environ 0,1 ms ? puissance (W) = énergie (J) / durée (s) = 6,75/10-4 = 6,75 104 W. La résistance du flash est-elle plus petite, égale, ou plus grande que celle de la résistance du conducteur ? La durée de la décharge est de l'ordre de 10-4 s. La constante de temps du circuit de décharge est donc de l'ordre de 10-4 s, c'est à dire 1000 fois plus petite que la constante de temps du circuit de charge. r est très inférieure à R.

retour -menu