Chute du contrepoids sur un ressort concours kiné APHP 2008

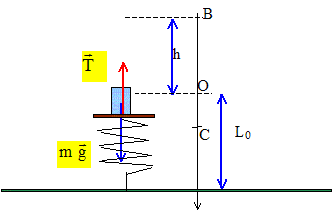
le contrepoids de mase m est lâché sans vitesse initiale d'une hauteur h au dessus d'un ressort à spires non jointives de constante de raideur k et de longueur à vide L0. On veut déterminer de quelle longueur OC = x1 le ressort se comprime, puis calculer son mouvement ultérieur lorsqu'il reste accroché au ressort vertical. La position du contrepoids est repérée par l'abscisse x. l'état de référence pour l'énergie potentielle correspond à la position O. Quelles sont les forces appliquées au contrepoids de masse m quand sa position est telle que x>0 ? Le contrepoids est soumis à son poids ( valeur mg) et à une force de rappel ( valeur kx ) exercée par le ressort.   En effectuant un bilan énegétique entre les positions B ( abscisse xB) et C ( abscisse xC), établir l'équation du second degré vérifiée par OC= x1. Le système est le contrepoids et le ressort. En B l'énergie mécanique est sous forme potentielle de pesanteur : mgh. En C l'énergie mécanique est sous forme potentielle de pesanteur et potetielle élastique : -mgx1 +½kx12. L'énergie mcanique se conserve en absence de frottement : -mgx1 +½kx12 = mgh ; ½kx12 -mgx1 -mgh=0. En appliquant la seconde loi de Newton au contrepoids, lorsque x >0, établir l'équation différentielle vérifiée pr x.  mg-kx=mx" ; x" +k/m x = g. On pose X = x-mg/k. Que devient l'équation différentielle précédente ? X" = x" ; x = X+ mg/k ; k/m x = k/m X + g d'où : X"+k/m X=0.   La solution de la nouvelle équation différentielle est de la forme X(t) = X0 sin (2pt/T0+j). En déduire l'expression de la période T0 en fonction de k et m. w0 = 2p/T0 avec w02 =k/m d'où T0 =2p(m/k)½. A partir de l'expression de X(t) donner l'expression de x(t). x = X+ mg/k ; x(t) = X0 sin (2pt/T0+j)+ mg/k. Quelle est l'abscisse xE=OE repérant la position d'équilibre ? A la position d'équilibre statique le poids et la tension du ressort ont la même valeur : mg = kxE d'où xE = mg/k. En prenant pour origine des dates l'instant où le contrepoids passe en E dans le sens descendant, déterminer la valeur de j. x(t) = X0 sin (2pt/T0+j)+ xE. x(0) = X0 sin (j)+ xE = xE ; X0 sin (j) avec X0 amplitude non nulle. sin (j) =0 soit j =0 ou j =p. Quelle est l'expression de la vitesse du contrepoids ? La vitesse est la dérivée de l'abscisse par rapport au temps. v(t) = x'(t) = X0 2p/T0 cos (2pt/T0). Pour quelle abscisse et à quelle date cette vitesse s'annule-t-elle pour la première fois pout t>0 ? cos (2pt/T0) = 0 ; 2pt/T0 = ½p d'où : t = 0,25 T0. En déduire l'expression de X0 en fonction de x1, m, k et g. à t = 0,25 T0, la vitesse est nulle et l'abscisse vaut x1. 2pt/T0 =2p/T0 * 0,25T0 =½p. x1 = X0 sin (½p)+ xE = X0 + xE ; X0 = x1-xE ; X0 = x1-mg/k.

retour -menu